Soluções da Edição Anterior

Problemas Universitários

Considere a matriz \(A = (a_{ij})_{i, j}^{n, n+1}\) (\(n\) linhas e \(n+1\) colunas) definida da seguinte maneira: \[a_{ij} = \begin{cases} 1, \ \ \mbox{se} \ i \in A_j \\ 0, \ \ \mbox{se} \ i \not\in A_j \end{cases}.\] Ou seja, dispomos os conjuntos \(A_1, \ldots, A_{n+1}\) como vetores colunas \(\overline{A}_1, \ldots, \overline{A}_{n+1}\) representando as indicadoras da \(n-\)upla ordenada \((1, 2, \ldots, n)\) em cada um dos conjuntos. Por hipótese, como cada um deles é não vazio, significa que os vetores colunas dessa matriz são não nulos.

Agora, sendo o posto da matriz \(A\) no máximo \(n\), então o números de colunas linearmente independentes é no máximo \(n\), de onde segue que, \(\overline{A}_1, \ldots, \overline{A}_{n+1}\) são linearmente dependentes. De onde segue que, existem números reais \(\alpha_1, \alpha_2, \ldots, \alpha_{n+1}\), não todos nulos, para os quais \[\alpha_1 \overline{A}_1 + \cdots + \alpha_{n+1} \overline{A}_{n+1} = 0.\]

Como todos esses vetores são não nulos e com entradas \(0\) ou \(1\) (não negativas), segue que existem entre esses escalares, alguns que são positivos \((\alpha_i > 0)\) e alguns que são negativos \((\alpha_j < 0)\). Considere então \(I\) e \(J\) os conjuntos destes escalares que são positivos e negativos, respectivamente (são não vazios e disjuntos). Daí, \[v = \sum_{i \in I} \alpha_i \overline{A}_i = \sum_{j \in J} (-\alpha_j) \overline{A}_j.\] Essa igualdade entre as duas representações do vetor \(v\) acima (que possui entradas não negativas), em termos dos conjuntos \(A_k\) significa que, se a entrada \(\ell\) de \(v\) é diferente de \(0\), então \(\ell \in A_i, A_j\) para algum \(i \in I\) e \(j \in J\). Agora, se a entrada \(\ell\) de \(v\) é igual a \(0\), então \(\ell \not\in A_i, A_j\) para todos \(i \in I\) e \(j \in J\). Ou seja, \[\displaystyle \bigcup_{i \in I} A_i = \bigcup_{j \in J} A_j.\]

Suponha que \((\mathbb{R},+)\) possui uma raiz \(X\) via um isomorfismo \(\phi\). Podemos considerá-la como um subgrupo aditivo de \(\mathbb{R}\) identificando \(X\) com a imagem por \(\phi\) de \(X \times {0}\). É simples de ver que \(X\), com as operações usuais, é um subespaço de \(\mathbb{R}\) sobre \(\mathbb{Q}\). De fato, dado qualquer natural \(q\) e um elemento \(x \in X\), existe \((a, b)\) em \(X \times X\) tal que \(q \cdot (a, b) = (x, 0)\) e, portanto, \(b = 0\). Assim, \(a \in X\) é tal que \(a = x/q\) e daí segue da estrutura de grupo que \(X\) é fechado por produto por escalar racional.
Disso segue que \(X\) é raiz de \(\mathbb{R}\), por analogia ao conceito definido no enunciado, também como estrutura de espaço vetorial sobre \(\mathbb{Q}\). Feito isso, note que se \(B\) é base de Hamel de \(X\), \(B \times \{0\} \cup \{0\} \times B\) é base de \(X \times X\) e suas imagens serão uma base de Hamel de \(\mathbb{R}\). Daí, o problema de achar uma raiz de \((\mathbb{R},+)\) resume-se a, dada uma base de Hamel \(H\) de \(\mathbb{R}\), encontramos um subconjunto \(B\) contido em \(H\) em bijeção com \(H \setminus B\).
Para isso, defina o conjunto dos pares \((C, f)\), \(C\) contido em \(H\) e \(f: C \to H \setminus C\) injetivas ordenado com \((C, f) \leq (D, g) \Leftrightarrow C \subset D\) e \(g\) estende \(f\). Esse conjunto satisfaz as condições do Lema de Zorn, logo tem um elemento maximal \((B, h)\). Agora, em virtude da maximalidade, \((H \setminus B) \setminus h(B)\) tem, no máximo, um elemento, e em ambos os casos de cardinalidades de \((H \setminus B) \setminus h(B)\), \(B\) é um subconjunto como pedimos no parágrafo acima.

Seja \(S = \sum_{i=1}^r M_i\). Para qualquer \(j\), a sequência \(M_jM_1, M_jM_2, \ldots, M_jM_r\) é uma permutação dos elementos de \(G\). Somando todos eles, obtemos \(M_jS = S\). Somando essas expressões de \(j = 1\) até \(r\) resulta em \(S^2 = rS\). Portanto, o polinômio minimal de \(S\) divide \(x^2 - rx\) e, consequentemente, todo autovalor de \(S\) é \(0\) ou \(r\). Por outro lado, soma dos autovalores, contados com multiplicidade, é \(\operatorname{tr}(S) = 0\), então todos os autovalores são iguais a \(0\). Todo autovalor de \(S - rI\) é \(-r \neq 0\), logo \(S - rI\) é invertível. Portanto, de \(S(S - rI) = 0\), obtemos \(S = 0\).

Dado o \(f(x)\) do enunciado, tem-se que \[f'(x) = a_1 \cdot \cos(x) + 2\cdot a_2 \cdot \cos(2x) +\ldots + n \cdot a_n \cdot \cos(nx).\] Daí, nota-se que \[\begin{aligned} f(0) & = a_1 \cdot sen(0) + a_2 \cdot sen(0) + \ldots + a_n \cdot sen(0) \\ & = 0; \\ f'(0) & = a_1 \cdot \cos(0) + 2\cdot a_2 \cdot \cos(0) + \ldots + n \cdot a_n \cdot \cos(0);\\ & = a_1 + 2 \cdot a_2 + \ldots + n \cdot a_n.\end{aligned}\] Portanto, basta mostrarmos que \(|f'(0)| \leq 1\). Pelo enunciado, \(|f(x)| \leq |\mathop{\mathrm{sen}}(x)|\), então supondo que \(x \neq 0\), tem-se que \[\left|\dfrac{f(x)}{x}\right| \leq \left|\dfrac{\mathop{\mathrm{sen}}(x)}{x}\right|.\] Daí \[|f'(0)| = \left|\lim_{x \to 0}\dfrac{f(x)-f(0)}{x-0}\right| \leq \left|\lim_{x \to 0}\dfrac{\mathop{\mathrm{sen}}(x)}{x}\right| = 1.\]

Denote o valor da integral acima por \(I\). Fazendo a mudança de variável \(u = \dfrac{\pi}{2} - x\), tem-se que \[\dfrac{\mathop{\mathrm{sen}}^{25}(x)}{\mathop{\mathrm{sen}}^{25}(x) + \cos^{25}(x)} = \dfrac{\cos^{25}(u)}{\cos^{25}(u) + \mathop{\mathrm{sen}}^{25}(u)}.\] Além do mais, \(du = -dx\) para \(x=0\) temos \(u = {\pi}/{2}\) e para \(x=\pi/{2}\), temos \(u = 0\). Daí, obtemos \[\begin{aligned} \int_{0}^{\pi/2}\dfrac{\mathop{\mathrm{sen}}^{25}(x)}{\mathop{\mathrm{sen}}^{25}(x) + \cos^{25}(x)}\ dx &= \\ -\int_{\pi/2}^{0}\dfrac{\cos^{25}(u)}{\mathop{\mathrm{sen}}^{25}(u) + \cos^{25}(u)}\ du &= \\ \int_{0}^{\pi/2}\dfrac{\cos^{25}(x)}{\mathop{\mathrm{sen}}^{25}(x) + \cos^{25}(x)}\ dx &.\end{aligned}\] Portanto, \(I + I = \int_0^{\pi/ 2}1 dx = \pi/2\) e, consequentemente, \(I = \dfrac{\pi}{4}\).

Problemas de Matemática Elementar

Problema 6. A figura a seguir consiste de \(5\) quadrados iguais colocados no interior de um retângulo \(8 cm \times 7 cm\). Qual a medida do lado desses quadrados?

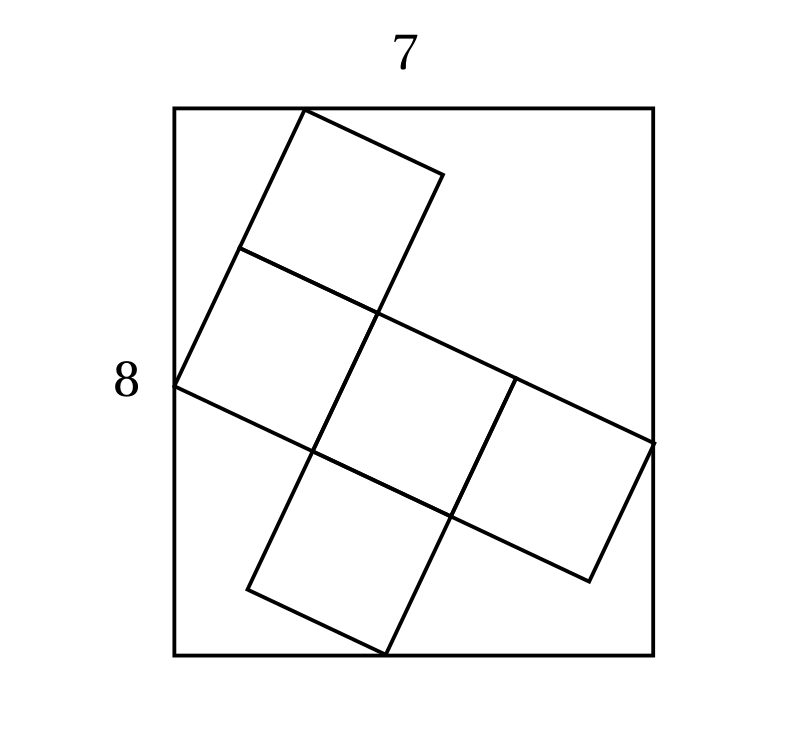
Seja \(a\) o comprimento do lado do quadrado. Como as inclinações dos lados dos quadrados formam \(90^{\circ}\) entre si, só existem dois comprimentos possíveis de projeções dos lados dos quadrados sobre os lados dos retângulos: \(x\) ou \(y\).

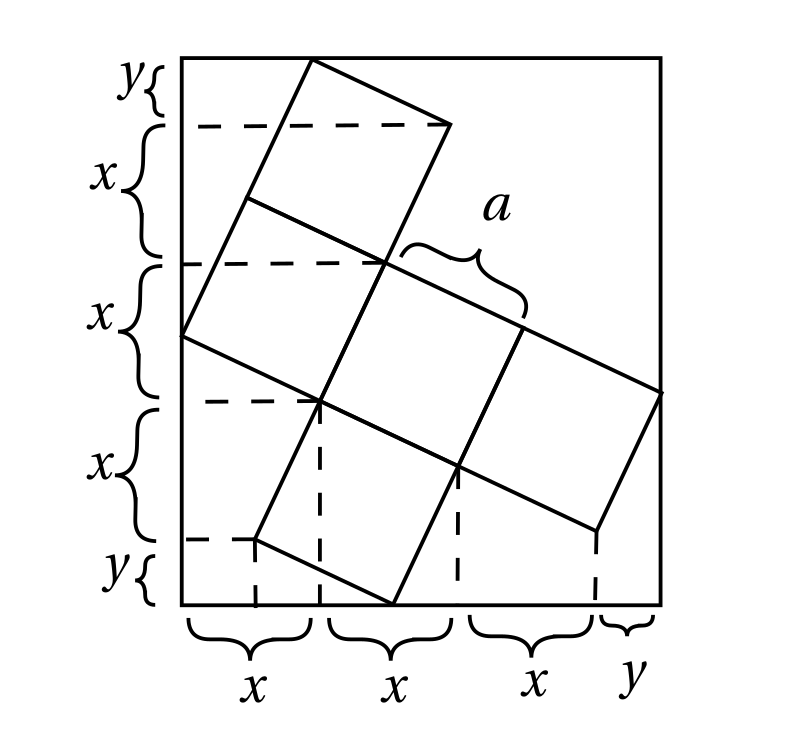
Comparando as medidas dos dois lados dos retângulos com essas projeções, temos \(8 = 2x+y+x+y=3x+2y\) e \(7 = 3x+y\). Resolvendo o sistema resultante, encontramos \(x=2\) e \(y=1\). Portanto, pelo Teorema de Pitágoras, \(a =\sqrt{x^2+y^2}=\sqrt{5}\, cm\).

Problema 7. Na figura a seguir, \(ABCD\) é um quadrado e \(M\), \(N\), \(P\) e \(Q\) são os pontos médios dos seus lados. As áreas de três regiões do seu interior são \(20\,cm^2\), \(32\,cm^2\) e \(16\,cm^2\), também como indicado na figura. Qual a área da quarta região?

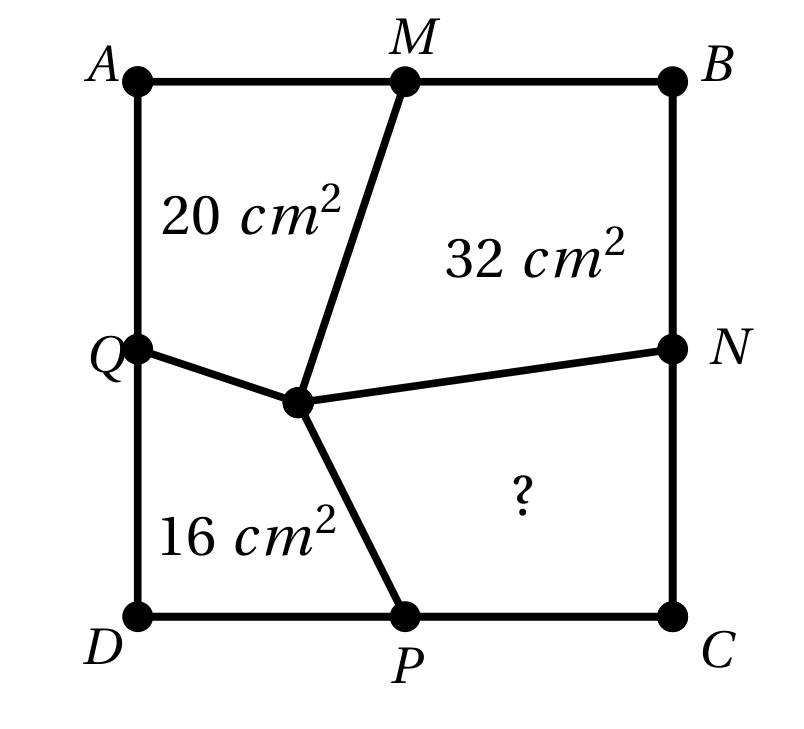
Seja \(R\) o ponto central da figura, \(2x\) o comprimento de metade de um lado do quadrado e \(d_1\), \(d_2\), \(d_3\) e \(d_4\) as distâncias de \(R\) aos lados.

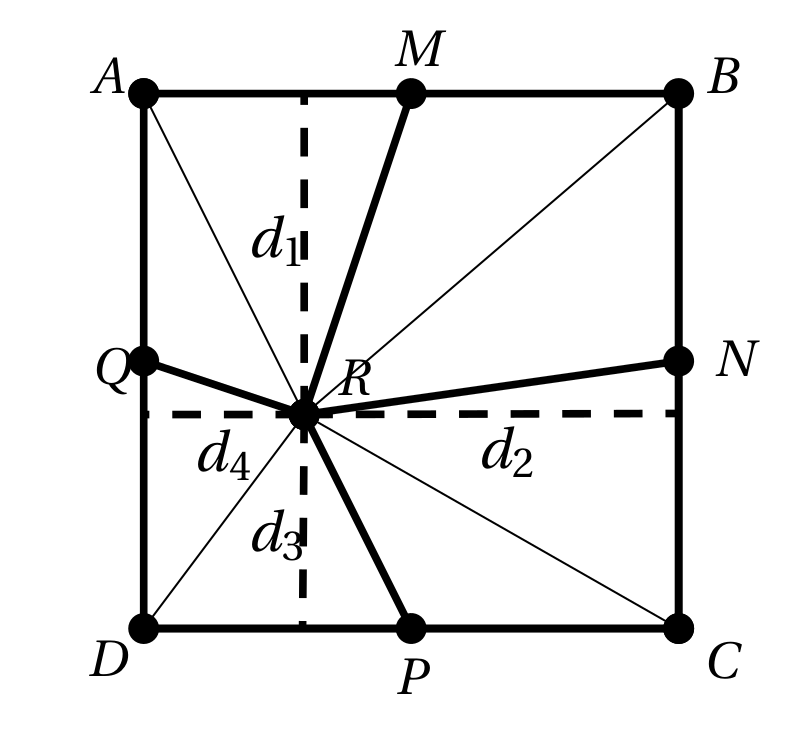
A área do quadrilátero \(DPRQ\) é a soma das áreas de dois triângulos de bases de comprimento \(2x\) e alturas \(d_3\) e \(d_4\). Ou seja, \[A_{DPRQ} = \dfrac{2x \cdot d_3}{2}+\dfrac{2x \cdot d_4}{2} = x \cdot (d_3+d_4) .\] De modo semelhante, \[A_{AQRM} = x \cdot (d_1+d_4), A_{BMRN} = x \cdot (d_1+d_2)\] \[\text{e }A_{CNRP} = x \cdot (d_2+d_3).\] Portanto, \[\begin{aligned} A_{CNRP} + A_{AQRM} & = & A_{BMRN} + A_{DPRQ} \\ A_{CNRP} + 20 & = & 32 + 16.\end{aligned}\] Assim, \(A_{CNRP} = 32+16-20 = 28\,cm^2\).

A desigualdade acima pode ser reescrita como: \[\begin{aligned} \dfrac{2010}{2011} < \frac{x}{y} < \dfrac{2011}{2012} &\Leftrightarrow \\ 1 - \dfrac{1}{2011} < 1 -\frac{t}{y} < 1 - \dfrac{1}{2012} &\Leftrightarrow \\ 2011 < \dfrac{y}{t} < 2012. \end{aligned}\] com \(t = y - x \in \mathbb{Z}\). Devemos ter \(t \geq 2\), pois para \(t = 1\) não existe um inteiro \(y\) tal que \(2011<y<2012\). Da desigualdade \(2011 \cdot t < y < 2012 \cdot t\), tem-se que \(y \geq 2011 \cdot t + 1\). Daí:

\[\begin{aligned} x + y & = (y - t) + y \\ & = 2y -t \\ & = 2\cdot (2011 \cdot t + 1) - t \\ & = 4021 \cdot t + 2.\end{aligned}\] Como \(t \geq 2\), tem-se que o menor valor possível para \(x+y\) é \[x + y = 4021 \cdot 2 + 2 = 8042 + 2 = 8044.\] Um exemplo é \(x = 4021\) e \(y=4023\).

Veja que \[a^2 + b^2 + c^2 + 2(ab + bc + ca) = (a + b + c)^2 = 0.\] De onde, \[ab + bc + ca = -2\] (pois \(a^2 + b^2 + c^2 = 4\)).

Assim, \[(ab)^2 + (bc)^2 + (ca)^2 + 2(ab^2c + bc^2a + ca^2b) =\] \[(ab + bc + ca)^2 = (-2)^2 = 4\] \[\therefore (ab)^2 + (bc)^2 + (ca)^2 + 2abc(a + b + c) = 4\] \[\therefore (ab)^2 + (bc)^2 + (ca)^2 = 4.\]

Note que, \[\begin{aligned} \frac{1}{\sqrt{n} + \sqrt{n+1}} &= \frac{\sqrt{n+1} - \sqrt{n}}{(\sqrt{n+1} + \sqrt{n})(\sqrt{n+1} - \sqrt{n})} \\ &= \frac{\sqrt{n+1} - \sqrt{n}}{n+1 - n} \\ &= \sqrt{n+1} - \sqrt{n}. \end{aligned}\] Assim, \[\begin{aligned} \sum_{n=1}^{99} \frac{1}{\sqrt{n} + \sqrt{n+1}} &= \sum_{n=1}^{99} \sqrt{n+1} - \sqrt{n} \\ &= \sqrt{100} - \sqrt{1} = 10 - 1 = 9.\end{aligned}\] Além disso, \[\frac{1}{1+\sqrt{2}} + \frac{1}{\sqrt{3}+\sqrt{4}} + \frac{1}{\sqrt{5}+\sqrt{6}} + \cdots + \frac{1}{\sqrt{99}+\sqrt{100}} =\] \[\sum_{k=0}^{49} \frac{1}{\sqrt{2k+1} + \sqrt{2k+2}} > \sum_{k=0}^{48} \frac{1}{\sqrt{2k+2} + \sqrt{2k+3}}\] e \[\sum_{k=0}^{49} \frac{1}{\sqrt{2k+1} + \sqrt{2k+2}} + \sum_{k=0}^{48} \frac{1}{\sqrt{2k+2} + \sqrt{2k+3}} =\] \[\sum_{n=1}^{99} \frac{1}{\sqrt{n} + \sqrt{n+1}} = 9.\] Portanto, \[2 \sum_{k=0}^{49} \frac{1}{\sqrt{2k+1} + \sqrt{2k+2}} > 9\] e \[\sum_{k=0}^{49} \frac{1}{\sqrt{2k+1} + \sqrt{2k+2}} > \frac{9}{2}.\]

Primeiramente vamos mostrar que qualquer sequência maximizante do número de inversões precisa ser não-crescente. De fato, se existe um par de números consecutivos \(a\) e \(b\), com \(a< b\), então a troca de posição desses elementos não altera a soma e aumenta o número de inversões em uma unidade. A seguir, mostraremos que qualquer sequência não-crescente que maximiza o número de inversões deve possuir apenas números iguais a \(1\) e \(2\). Suponha, por absurdo, que a sequência contém algum número \(k>2\). Troque o último \(k\) por um par de elementos: \(k-1\) na posição original e \(1\) na posição final. Claramente essa operação não altera a soma. O \(1\) final é parte de uma inversão com todo o elemento que era membro de uma inversão com o \(k\) original, exceto pelos números \(1\) a sua direita. O novo \(k-1\) é parte de uma inversão com todo elemento que era menor que o \(k\) original, incluindo as parcelas \(1\) a sua direita. Assim, contabilizando a inversão criada entre o novo \(k-1\) e o novo \(1\), essa troca criada aumenta o número de inversões em pelo menos uma unidade. Finalmente, considerando uma sequência qualquer que maximiza o número de inversões e que possui de soma de seus elementos igual a \(2019\), podemos supor que existem \(a\) parcelas iguais a \(2\) e \(2019-2a\) parcelas iguais a \(1\). O número de inversões é \[\begin{aligned} a(2019-2a) & = & 2019a-2a^2 \\ & = & \dfrac{2019^2}{8} - 2\left ( a-\dfrac{2019}{4} \right )^2.\end{aligned}\] Para maximizar a expressão anterior, devemos minimizar \(|a-2019/4|\) e isso ocorre para \(a=505\). Portanto, o maior número de inversões é \(505 \cdot 1009\).

Provaremos esse resultado por indução. Vejamos.

Se \(n=1\), temos \(x_1 = \frac{1}{2}\) e então \(\frac{1-x_1}{1+x_1} = \frac{1/2}{3/2} = \frac{1}{3}\).

Agora, vamos supor que a afirmação é válida para \(n\), e suponhamos que \(x_1, x_2, \ldots, x_n, x_{n+1}\) são números positivos para os quais \(x_1 + \cdots + x_n + x_{n+1} = \frac{1}{2}\).

Primeiro vejamos o seguinte: se \(0 < a \leq b\) e \(c \geq 0\), então \(bc \geq ac\) e \((a+c)b = ab + bc \geq ab + ac = (b+c)a\) e portanto, \(\frac{a+c}{b+c} \geq \frac{a}{b}\). Aplicando esse fato aos números \(a=1-(x_n+x_{n+1}), \ b=1+(x_n+x_{n+1})\) e \(c=x_nx_{n+1}\), segue que \[\frac{1-(x_n+x_{n+1}) + x_nx_{n+1}}{1+(x_n+x_{n+1}) + x_nx_{n+1}} \geq \frac{1-(x_n+x_{n+1})}{1+(x_n+x_{n+1})}.\] Portanto, \[\frac{1-x_n}{1+x_n} \cdot \frac{1-x_{n+1}}{1+x_{n+1}} \geq \frac{1-(x_n+x_{n+1})}{1+(x_n+x_{n+1})}.\]

Agora, fazendo \(y_n = x_n + x_{n+1}\), temos que \(x_1, \ldots, x_{n-1}, y_n\) são \(n\) números positivos cuja soma é igual a \(\frac{1}{2}\), e por hipótese de indução vale que, \[\frac{1-x_1}{1+x_1} \cdot \frac{1-x_2}{1+x_2} \cdots \frac{1-y_n}{1+y_n} \geq \frac{1}{3},\] isto é, \[\frac{1-x_1}{1+x_1} \cdot \frac{1-x_2}{1+x_2} \cdots \frac{1-(x_n+x_{n+1})}{1+(x_n+x_{n+1})} \geq \frac{1}{3}.\] Por \((1)\) e \((2)\), segue que, \[\frac{1-x_1}{1+x_1} \cdot \frac{1-x_2}{1+x_2} \cdots \frac{1-x_n}{1+x_n} \cdot \frac{1-x_{n+1}}{1+x_{n+1}} \geq \frac{1}{3}\] e por indução, a afirmação é vale para todo \(n \geq 1\), de onde segue o desejado.

Novos Problemas

Problemas Universitários

Problemas de Matemática Elementar