Solução 1. Observe a figura a seguir. Se o vértice \(A\) é o afixo do número complexo \(z_1\), segue que o vértice \(B\) corresponde ao afixo do número complexo \(iz_1\).(O número complexo cujo afixo é o ponto \(B\) é obtido de \(z_1\) por uma rotação de \(90^o\) no sentido anti-horário, o que é obtido por uma multiplicação por \(i\)).

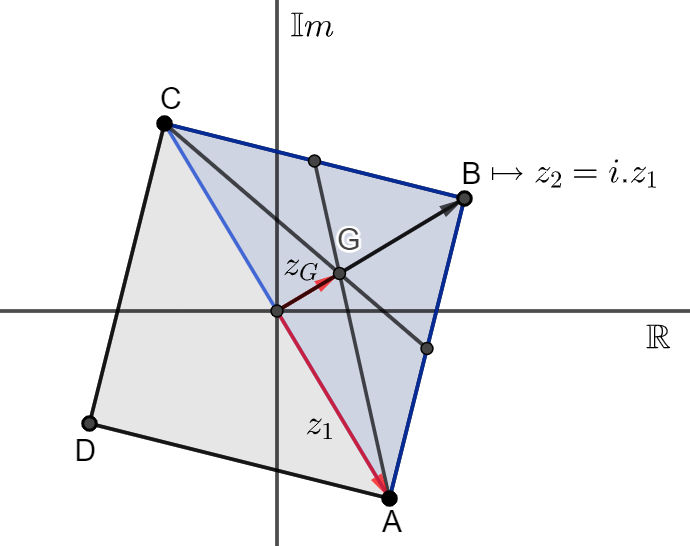
Por fim, como o triângulo \(ABC\) é isósceles de base \(AC\), segue que \(OB\) é uma das medianas do triângulo. Sendo \(G\) o braricentro do triângulo \(ABC\), segue que \(OG=\frac{1}{3}OB \Rightarrow z_G=\frac{1}{3}i.z_1\) (onde \(z_G\) é o número complexo cujo afixo é o ponto \(G\)). Diante do exposto, \[z_G=\frac{1}{3} \cdot z_1=\frac{z_3}{3}\left(cos\frac{\pi}{2}+isen\frac{\pi}{2}\right).\]

Solução 2. A função \(f(n)\) que conta tais pares com \(n\) no lugar de 6000 é multiplicativa, ou seja, \(f(mn) = f(m)f(n)\) se \(m,n\) são primos entre si. Daí é fácil ver que \(f(n) =n \cdot \prod_{p\mid n} (1 + \frac{1}{p})\) com \(p\) primo.

Solução 3. Vamos trabalhar no anel de polinômios \(\mathbb{F}_2[x]\), em que \(\mathbb{F}_2\) é o corpo dos inteiros módulo 2. Neste anel, temos \[x^5 \equiv x^2 + 1 \pmod{x^5 + x^2 + 1}\] implica que \[x^{10} \equiv (x^2 + 1)^2 \equiv x^4 + 1 \pmod{x^5 + x^2 + 1},\] ou seja, \[\begin{aligned} x^{20} &\equiv (x^4 + 1)^2 \\ & \equiv x^8 + 1 \equiv x^3 (x^2+1) + 1 \\ &\equiv x^2 + x^3 \pmod{x^5 + x^2 + 1} \end{aligned}\] e portanto, módulo \(x^5 + x^2 + 1\), \[\begin{aligned} x^{30} &\equiv& (x^2 + x^3)\cdot (x^4 + 1) \\ &\equiv& x^7 + x^6 + x^3 + x^2\\ &\equiv& x^2(x^2+1) + x(x^2+1) + x^3 + x^2\\ &\equiv& x^4 + x\\ \implies x^{31} &\equiv& x^5 + x^2 \\ &\equiv& 1\end{aligned}\] (Uma maneira mais rápida de obter a última congruência seria perceber que \(x^5 + x^2 + 1\) é irredutítvel em \(\mathbb{F}_2[x]\), logo \(\mathbb{F}_2[x]/(x^5 + x^2 + 1)\) é um corpo, extensão de \(\mathbb{F}_2\) de grau 5, logo possui \(2^5 = 32\) elementos e por Lagrange \(a^{31} \equiv 1 \pmod{x^5 + x^2 + 1}\) se \(a\not\equiv 0 \pmod{x^5 + x^2 + 1}\)). Por fim, \(x^{2046} \equiv (x^{31})^{66} \equiv 1 \implies x^{2050} \equiv x^4\). Assim, \(r(x)\) é congruente a \(x^4\) módulo \(2\) e possui apenas 1 coeficiente ímpar.

Solução 4. A descrição de tal lugar geométrico \(\Gamma\) é de uma cônica com excentricidade \(e = \frac{c}{a} = \frac{1}{2}\), ou seja, \(\Gamma\) é uma elipse. Além disso, um dos focos dessa elipse é a origem e a reta \(y = -1\) é uma diretriz. Assim, o eixo focal (sendo perpendicular à diretriz) é vertical, paralelo ao eixo \(y\). De onde, o eixo focal é o próprio eixo \(y\). Assim, a maior distância entre dois pontos de \(\Gamma\) é exatamente o dobro do comprimento do semieixo maior, isto é, \(2a\).

Para completar, sendo \(A\) o vértice da elipse que está entre o foco \(F_1 = (0,0)\) e a diretriz \(r : y=-1\), temos \[1 + \frac{ d(A,r)}{d(A,F_1)} = \frac{d(A,F_1) + d(A,r)}{d(A,F_1)} = \frac{d(F_1,r)}{d(A,F_1)} = \frac{1}{d(A,F_1)}\] e \[a - c = d(A,F_1) = \frac{1}{1 + \frac{1}{e}} = \frac{1}{1+2} = \frac{1}{3}.\] Também, \[\frac{c}{a} = \frac{1}{2} \ \ \Rightarrow \ \ c = \frac{a}{2}.\] Então, \(a - \frac{a}{2} = \frac{1}{3}\) e \(a = \frac{2}{3}\). De onde, a máxima distância procurada é \(2a = \frac{4}{3}\).

Solução 5. Como \(f(f(x)) = x\) para todo \(x \in \mathbb{R}\), então \(f'(f(x)) \cdot f'(x) = 1\). De onde, \(f'(x) \neq 0\), para todo \(x \in \mathbb{R}\).

Agora, se existisse \(a\) tal que \(f'(a) > 0\) e como \(f'(0) = -1\), teríamos \[-1 = f'(0) < 0 < f'(a).\] Então, pelo Teorema de Darboux (valor intermediário para a derivada), existiria \(b\) entre \(0\) e \(a\) tal que \(f'(b) = 0\), o que contraria o que acabamos de descobrir acima. Portanto, \(f'(x) < 0\) para todo \(x \in \mathbb{R}\), e \(f\) é estritamente decrescente.

Assim, se \(f(x) > -x\) para algum \(x\), então \(x = f(f(x)) < f(-x) = -f(x)\), isto é, \(f(x) < -x\) , sendo uma contradição. Analogamente, não pode ocorrer \(f(x) < -x\). Portanto, \(f(x) = -x\) para todo \(x \in \mathbb{R}\).

Solução 6. Queremos mostrar que \[\mbox{rank}(A) + \mbox{rank}(B) \leq n \ \ \ \ \Leftrightarrow \ \ \ \ \exists X \ \mbox{invertível} \ : \ AXB = O_n\]

\(( \ \Leftarrow \ ) :\) Supondo a existência de uma matriz invertível \(X\) satisfazendo \(AXB = O_n\), pela desigualdade de Sylvester para o posto de matrizes, tem-se \[0 = \mbox{rank}(O_n) = \mbox{rank}(AXB) \geq \mbox{rank}(A) + \mbox{rank}(XB) - n\] e \[\mbox{rank}(XB) \geq \mbox{rank}(B) + \mbox{rank}(X) - n\] \[= \mbox{rank}(B) + n - n = \mbox{rank}(B).\]

Daí, \(0 \geq \mbox{rank}(A) + \mbox{rank}(B) - n\), ou seja, \(\mbox{rank}(A) + \mbox{rank}(B) \leq n\).

\(( \ \Rightarrow \ ) :\) Estamos supondo agora que \(\mbox{rank}(A) + \mbox{rank}(B) \leq n\). Existem matrizes inversíveis \(X_A, Y_A, X_B\) e \(Y_B\) tais que \[Y_A \cdot A \cdot X_A = \begin{bmatrix} I_{\mbox{rank}(A)} & \ \ 0 \\ 0 & \ \ O_{n - \mbox{rank}(A)} \end{bmatrix}\] e \[X_B \cdot B \cdot Y_B = \begin{bmatrix} O_{n - \mbox{rank}(B)} & \ \ 0 \\ 0 & \ \ I_{\mbox{rank}(B)} \end{bmatrix}\] onde \(I_{\mbox{rank}(A)}\) e \(I_{\mbox{rank}(B)}\) são matrizes identidades de ordens \(\mbox{rank}(A)\) e \(\mbox{rank}(B)\), respectivamente. E \(0\) ali representam matrizes nulas com as devidas ordens para preencherem as entradas restantes. Assim, multiplicando \(Y_A \cdot A \cdot X_A\) e \(X_B \cdot B \cdot Y_B\), obtemos \[\begin{bmatrix} I_{\mbox{rank}(A)} & \ \ 0 \\ 0 & \ \ O_{n - \mbox{rank}(A)} \end{bmatrix} \cdot \begin{bmatrix} O_{n - \mbox{rank}(B)} & \ \ 0 \\ 0 & \ \ I_{\mbox{rank}(B)} \end{bmatrix} = O_n\] essa última igualdade ocorre pois \(n - \mbox{rank}(B) \geq \mbox{rank}(A)\) e \(n - \mbox{rank}(A) \geq \mbox{rank}(B)\).

Portanto, tomando \(X = X_A \cdot X_B\) (que é invertível), obtemos \[AXB = Y_A^{-1} \cdot O_n \cdot Y_B^{-1} = O_n.\]

Solução 7. Como são oito dias de evento, ela não pode ter ganho mais que \(8\) medalhas de prata. Veja que essa quantidade não satisfaz o enunciado, pois \(8 \cdot 3 = 24 < 27\). Assim, ela obteve menos de \(8\) medalhas de prata. Vamos analisar os casos possíveis para determinar o número máximo de medalhas de prata que ela pode obter:

1. Se ela tivesse obtido \(7\) medalhas de prata, teria que fazer \(27-3 \cdot 7 = 6\) pontos em um dia de evento, mas isso não é possível.

2. Se ela tivesse obtido \(6\) medalhas de prata, teria que fazer \(27 - 3 \cdot 6 = 9\) pontos em dois dias de evento, mas isso não é possível pois \(5+3<9<5+5\).

3. Se ela tivesse obtido \(5\) medalhas de prata, teria que fazer \(27 - 3 \cdot 5 = 12\) pontos em três dias de evento. Como \(12> 3 \cdot 3\), pelo menos uma medalha de ouro, valendo \(5\) pontos, teria que ser obtida. Por outro lado, não é possível combinar apenas duas parcelas de \(1\), \(3\) e \(5\) para obter os \(12-5 = 7\) pontos restantes. Consequentemente, ela não pode ter obtido \(5\) medalhas de prata.

Para mostrar que \(4\) medalhas de prata é o máximo, basta exibirmos um exemplo. Após obter \(3 \cdot 4 = 12\) pontos em \(4\) dias com medalhas de prata, ela precisaria ter obtido \(27 - 3 \cdot 4 = 15\) pontos nos outros \(4\) dias. Luciana pode obter essa pontuação com \(3\) medalhas de ouro em \(3\) dias e \(1\) dia sem premiação.

Solução 8. Qualquer pessoa que afirme estar bebendo café necessariamente precisa ser italiana. Portanto, existem \(44\) italianos e \(11\) britânicos. Qualquer pessoa que afirme ser italiano tem que estar bebendo café. Portanto, havia 33 pessoas bebendo café. Seja \(n\) o número de britânicos bebendo café. Então existiam \(11-n\) britânicos bebendo chá, \(33-n\) italianos bebendo café e \(44-(33-n)=11+n\) italianos bebendo chá. Se não estava chovendo no lado de fora, então \(n+(11+n)=22\), mas \(n\) não é um inteiro nesse caso. Portanto, estava chovendo no exterior e \((11-n)+(33-n)=22\), consequentemente, \(n=11\). Segue daí que \(0\) britânicos estavam bebendo chá.

Solução 9. Se \(x\), \(y\) e \(z\) são as quantias de notas de \(\$20\), \(\$50\) e \(\$100\), respectivamente, portanto \(2x+5y+10z=80\). Como temos uma nota de cada tipo, podemos descontar uma \(1\) unidade de cada uma das incógnitas anteriores e reduzir a equação para \(2a+5b+10c=63\). Como \(63\) é ímpar, precisamos que \(b\) seja ímpar. Podemos analisar os casos. Quando \(b=1\), \(2a+10c=58\). Daí \(10c=0,10,20,30,40\) ou \(50\), ou seja, temos \(6\) soluções. Quando \(b=3\), \(2a+10c=48\) e daí \(10c=0,10,20,30\) ou \(40\), ou seja, temos \(5\) soluções. Continuando essa contagem, para \(b=5\), \(7\), \(9\) e \(11\), teremos \[6+5+4+3+2+1=21\] soluções.

Solução 10. (Solução de Yan Lima Machado) Seja \(BC=x\). Pelo Teorema de Pitágoras, tem-se que: \[\begin{aligned} AB & = & \sqrt{5}x\\ AC & = & \sqrt{8}x \\ DF & = & \sqrt{10}x \\\end{aligned}\]

Ademais, considere \(\angle BAC=\alpha\) e \(\angle EDF=\beta\). Temos \(\cos(\beta)=\frac{3x}{\sqrt{10}x}=\frac{3}{\sqrt{10}}\) e, pela Lei dos Cossenos no triângulo \(ABC\), \(x^{2}=8x^{2}+5x^{2}-4\sqrt{10}x^{2}\cos(\alpha)\), ou seja, \(\cos(\alpha)=\dfrac{12x^2}{4\sqrt{10}x^2} = \frac{3}{\sqrt{10}}\). Como \(\alpha, \beta \in (0,\pi/2)\) e \(\cos \alpha = \cos \beta\), segue que \(\alpha = \beta\).

Segunda Solução: Note que \(DH = HF\), pois ambos são diagonais de um retângulo \(2 \times 1\) e, além disso, \(\angle IHF = \angle IDH\).

Portanto, \[\angle DHF = \angle DHI + \angle IHF = \angle DHI + \angle HDI = 90^{\circ}.\] Assim, \(AGC\) e \(DHF\) são ambos triângulos retângulos isósceles. Como os triângulos \(AGB\) e \(DHI\) são congruentes, segue que \[\angle BAC = 45^{\circ} - \angle BAG = 45^{\circ} - \angle HDI = \angle FDE.\]

Solução 11. (Solução de Yan Lima Machado) Considere a medida dos lados dos triângulos igual a \(x\) e sejam \(D\), \(E\), e \(F\) os vértices marcados na figura a seguir.

Como o triângulo \(AEC\) é retângulo em \(E\), pois \(AE\) é mediatriz de um dos segmentos da malha, temos pelo Teorema de Pitágoras: \[\begin{aligned} AC^2 & = & AE^2 + EC^2 \\ & = & 3x^2+ 25x^2 \\ & = & 28x^2.\end{aligned}\] Pela Lei dos Cossenos nos triângulos \(ADB\) e \(BCF\), temos \[\begin{aligned} AB^2 & = & AD^2-2AD \cdot DB \cdot \cos 120^{\circ} + DB^2 \\ & = & x^{2}-2\cdot4x^{2}(\frac{-1}{2}) +16x^{2}\\ & = & 21x^2\end{aligned}\] e \[\begin{aligned} BC^2 & = & CF^2-2CF \cdot FB \cdot \cos 120^{\circ} + FB^2 \\ & = & x^{2}-2\cdot2x^{2}(\frac{-1}{2})+4x^{2}\\ & = & 7x^2.\end{aligned}\] Como \(AC^2=AB^2+BC^2\), pela recíproca do Teorema de Pitágoras, temos que \(\angle ABC=90^{\circ}\)

Segunda Solução: Continue o ladrilhamento com triângulos equiláteros como na figura anterior.

Note que o segmento \(CB\) é a diagonal de um paralelogramo formado por \(4\) triângulos do reticulado e, por simetria, o seu prolongamento irá encontrar o vértice \(D\) de outro paralelogramo também formado por \(4\) triângulos do reticulado. Tanto \(AD\) quanto \(AC\) são diagonais de paralelogramos congruentes, que estão pintados de cinza no desenho, portanto, \(AC = AD\). Assim, como \(B\) é o ponto médio de \(CD\), o segmento \(AB\) é uma altura do triângulo isósceles \(ACD\) e daí \(\angle ABC = 90^{\circ}\).

Solução 12. Se \[K = \frac{1}{2}\cdot \frac{3}{4} \cdot \frac{5}{6} \cdots \frac{99}{100},\] temos \[K > \frac{1}{2}\cdot \frac{2}{3} \cdot \frac{4}{5} \cdots \frac{98}{99}.\] Portanto, multiplicando a igualdade anterior por essa última desigualdade, obtemos: \[K^2 > \dfrac{1}{200} > \dfrac{1}{225},\] ou seja, \[K > \dfrac{1}{15}.\]

Agora, para mostrar a outra desigualdade do problema, temos

\[\begin{aligned} K & =& \frac{1}{2} \cdot \frac{3}{4} \cdot \frac{5}{6} \cdot \frac{7}{8}\cdots \frac{97}{98}\cdot \frac{99}{100} \\ &<& \frac{1}{2} \cdot \frac{3}{4} \cdot \frac{5}{6} \cdot \left(\frac{8}{9} \cdots \frac{98}{99} \cdot \frac{100}{101} \right)\cdot \frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7} \cdot \frac{3}{2} \cdot \frac{5}{4} \cdot \frac{7}{6} \\ &=& \frac{1}{2} \cdot \frac{3}{4} \cdot \frac{5}{6} \cdot \frac{3}{2} \cdot \frac{5}{4} \cdot \frac{7}{6} \cdot \left(\frac{2}{3} \cdot \frac{4}{5} \cdot \frac{6}{7} \cdot \frac{8}{9} \cdots \frac{98}{99} \cdot \frac{100}{101} \right)\end{aligned}\] O último membro pode ser reescrito como \[\frac{1}{2} \cdot \frac{3}{4} \cdot \frac{5}{6} \cdot \frac{3}{2} \cdot \frac{5}{4} \cdot \frac{7}{6} \cdot \frac{1}{101K} = \frac{175}{16 \cdot 16 \cdot 101K}\] Daí, \[K^2 < \frac{175}{16 \cdot 1616} < \frac{175}{16 \cdot 1575} = \frac{175}{16 \cdot 9 \cdot 175} = \frac{1}{144} = \frac{1}{12^2}\] e, portanto, \(K < \frac{1}{12}\). Logo, \[\frac{1}{15} < K < \frac{1}{12}.\]

Solução 13. Queremos simplicar ao máximo a expressão da soma \[\frac{2}{0! + 1! + 2!} + \frac{3}{1! + 2! + 3!} + \cdots + \frac{2024}{2022! + 2023! + 2024!} .\]

Veja que \[\frac{k}{(k-2)! + (k-1)! + k!} = \frac{k}{(k-2)! \cdot [1 + (k-1) + (k-1)k]}\] \[= \frac{k}{(k-2)! \cdot (k + k^2 - k)} = \frac{k}{(k-2)!k^2} = \frac{k-1}{(k-2)!(k-1)k}\] \[= \frac{k-1}{k!} = \frac{1}{(k-1)!} - \frac{1}{k!}.\]

Daí, \[\sum_{k=2}^{2024} \ \ \frac{k}{(k-2)! + (k-1)! + k!} = \sum_{k=2}^{2024} \ \ \frac{1}{(k-1)!} - \frac{1}{k!}\] é uma soma telescópica. Com isso, \[\frac{2}{0! + 1! + 2!} + \frac{3}{1! + 2! + 3!} + \cdots + \frac{2024}{2022! + 2023! + 2024!}\] \[= \left( 1 - \frac{1}{2!} \right) + \left( \frac{1}{2!} - \frac{1}{3!} \right) + \cdots + \left( \frac{1}{2023!} - \frac{1}{2024!} \right) = 1 - \frac{1}{2024!}.\]

Também recebemos uma solução correta de Yan Lima Machado