Problema
O Encontro na Cafeteria e Outros Problemas
Soluções da Edição Anterior
Problema 1. Calcule o valor de \(\int_0^{\pi/2} \frac{dx}{1 + (\mathop{\rm tg}x)^{2022}}\) é
Solução 1. Seja \[\begin{aligned} I & = & \int_0^{\pi/2} \frac{dx}{1 + (\mathop{\rm tg}x)^{2022}} \\ & = & \int_0^{\pi/2} \frac{(\cos x)^{2022} dx}{(\mathop{\mathrm{sen}}x)^{2022} + (\cos x)^{2022}} \end{aligned}\]
Com a mudança de variável \(y=\pi/2-x\), temos \(dy = -dx\) e
\[\begin{aligned} I & = & \int_{\pi/2}^0 \frac{(\cos (\pi/2-y))^{2022} (-dy)}{(\mathop{\mathrm{sen}}(\pi/2-y))^{2022} + (\cos (\pi/2-y))^{2022}} \\ & = & \int_0^{\pi/2} \frac{(\mathop{\mathrm{sen}}y)^{2022} dy}{(\mathop{\mathrm{sen}}y)^{2022} + (\cos y)^{2022}} \end{aligned}\] Portanto, \[I + I = \int_0^{\pi/2} \frac{(\mathop{\mathrm{sen}}x)^{2022}+(\cos x)^{2022} dx}{(\mathop{\mathrm{sen}}x)^{2022}+(\cos x)^{2022}} = \dfrac{\pi}{2}.\] Assim, \(I=\dfrac{\pi}{4}\).
Problema 2. Encontre o valor de
\[\displaystyle \int_0^{\pi/2} \cos^2 (\cos x)dx + \int_0^{\pi/2} \mathop{\mathrm{sen}}^2 (\mathop{\mathrm{sen}}x)dx .\]
Solução 2. Com a mudança de variável \(y=\pi/2-x\), temos \(dy = -dx\) e \[\begin{aligned} \int_0^{\pi/2} \mathop{\mathrm{sen}}^2 (\mathop{\mathrm{sen}}x)dx & = & \int_{\pi/2}^{0} \mathop{\mathrm{sen}}^2 (\mathop{\mathrm{sen}}(\pi/2-y))(-dy) \\ & = & \int_{0}^{\pi/2} \mathop{\mathrm{sen}}^2 (\cos y)dy \\ \end{aligned}\] Como \(\cos^2 (\cos x)+\mathop{\mathrm{sen}}^2(\cos x)=1\), segue que \[\begin{aligned} \int_0^{\pi/2} \cos^2 (\cos x)dx + \int_0^{\pi/2} \mathop{\mathrm{sen}}^2 (\mathop{\mathrm{sen}}x)dx & = & \\ \int_0^{\pi/2} \cos^2 (\cos x)dx + \int_0^{\pi/2} \mathop{\mathrm{sen}}^2 (\cos x)dx & = & \\ \int_0^{\pi/2} 1 dx & = & \pi/2 \end{aligned}\]
Problema 3. Seja \(A_{2022} = (a_{ij})\) a matriz \(2022 \times 2022\) definida por
\[a_{ij} = \left \{ \begin{array}{cl} \sqrt{3}, & \text{se}\,\,i=j \\1, & \text{se}\,\,|i-j|=1 \\ 0 & \text{caso contrário} \end{array} \right .\]
Encontre o valor de \(\det A_{2022}\).
Solução 3. Defina como \(A_n\) uma matriz \(n \times n\) definida pelas mesmas regras e seja \(D_n = \det A_n\). Pelo desenvolimento do determinante pela regra de Laplace com relação a primeira linha, temos \[D_n = \sqrt{3}D_{n-1}-D_{n-2}.\] A equação característica é
\[x^2-\sqrt{3}x+1=0,\]
que possui como raízes \(\dfrac{\sqrt{3}\pm i}{2} = -iw\) ou \(iw^2\). Aqui \(w=\dfrac{-1+i\sqrt{3}}{2}\) é raíz cúbica da unidade, i.e, \(w^3=1\). Resolvendo a recorrência, encontramos \[D_n = \dfrac{(-iw)^{2n+2}-1}{(-iw)^n((-iw)^2-1)}\] Daí, usando que \(w^3=1\) e \(w^2+w+1=0\), temos \[\begin{aligned} D_{2022} & = & \dfrac{(-iw)^{4046}-1}{(-iw)^{2022}((-iw)^2-1)} \\ & = & \dfrac{-w^2-1}{-(-w^2-1)} \\ & = & \dfrac{w}{-w} \\ & = & -1. \end{aligned}\]
Problema 4. Sejam \(z = e^{\frac{2\pi i}{2023}} = \cos \frac{2\pi}{2023} + i\mathop{\mathrm{sen}}\frac{2\pi}{2023}\), \[A = \{1, z, z^2, \ldots, z^{2022} \}\] e \[B = \{1, 1+z, 1+z+z^2, \ldots, 1+z+z^2+ \ldots+ z^{2022} \}.\]
Determine o número de elementos de \(A \cap B\).
Solução 4. Provaremos que \(A \cap B = \{1\}\). Inicialmente, é claro que \(1 \in A \cap B\). Por outro lado, veremos que não há outros elementos na interseção. Para isso, vamos mostrar que \(|1 + z + z^2 + \ldots + z^n| \neq 1\) para todo \(1 \le n \le 2022\). Veja que \[1 + z + z^2 + \ldots + z^n = \frac{z^{n+1}-1}{z-1}\] e, portanto, \[|1 + z + z^2 + \ldots + z^n| = \frac{|z^{n+1}-1|}{|z-1|}.\] Usando que \(e^{i\theta}-1 = 2i \mathop{\mathrm{sen}}(\theta/2)e^{i\theta/2}\), segue que \[|1 + z + z^2 + \ldots + z^n| = \frac{\sin\left(\frac{(n+1)\pi}{2023}\right)}{\sin\left(\frac{\pi}{2023}\right)}.\] Para \(1 \le n \le 2022\), temos que \(\mathop{\mathrm{sen}}((n+1)\pi/2023) \ge 0\) e \(\mathop{\mathrm{sen}}(\pi/2023) > 0\). Dessa forma, só poderíamos ter \(|1 + z + z^2 + \ldots + z^n| = 1\) caso \(\mathop{\mathrm{sen}}((n+1)\pi/2023) = \mathop{\mathrm{sen}}(\pi/2023)\), o que é impossível para \(1 \le n \le 2022\).
Problema 5. O famoso Problema da Basileia1 nos permite descobrir que
\[\dfrac{\pi^2}{8} = \dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+\ldots .\]
Vamos usar a série anterior para encontrar a soma de outra série. Para cada \(n \in \mathbb{N}\), defina como \(a_n\) seu maior divisor positivo ímpar. Por exemplo, \(a_{30} = 15\) e \(a_{24}=3\). Encontre o valor da soma:
\[S = \dfrac{a_1}{1^3}+\dfrac{a_2}{2^3}+\dfrac{a_3}{3^3}+\ldots .\]
Solução 5. Considere as séries geométricas
\[\begin{aligned} \dfrac{1}{1^3}+\dfrac{1}{(1\cdot 2)^3}+\dfrac{1}{(1\cdot 2^2)^3}+\dfrac{1}{(1\cdot 2^3)^3} + \ldots & = & \dfrac{8}{7} \\ \dfrac{1}{1^3}+\dfrac{1}{(3\cdot 2)^3}+\dfrac{1}{(3\cdot 2^2)^3}+\dfrac{1}{(3\cdot 2^3)^3} + \ldots & = & \dfrac{8}{7} \cdot \dfrac{1}{3^2} \\ \dfrac{1}{5^3}+\dfrac{1}{(5\cdot 2)^3}+\dfrac{1}{(5\cdot 2^2)^3}+\dfrac{1}{(5\cdot 2^3)^3} + \ldots & = & \dfrac{8}{7} \cdot \dfrac{1}{5^2} \\ \dfrac{1}{7^3}+\dfrac{1}{(7\cdot 2)^3}+\dfrac{1}{(7\cdot 2^2)^3}+\dfrac{1}{(7\cdot 2^3)^3} + \ldots & = & \dfrac{8}{7} \cdot \dfrac{1}{7^2} \\ & \vdots & \end{aligned}\] Cada fração \(\dfrac{a_n}{n^3}\) aparece exatamente uma vez em cada uma dessas séries. Portanto, a soma desejada é:
\[\dfrac{8}{7} \cdot \left ( \dfrac{1}{1^2}+ \dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2} + \ldots \right ) = \dfrac{8}{7} \cdot \dfrac{\pi^2}{8} =\dfrac{\pi^2}{7}.\]
Problema 6. Bernardo está brincando de desenhar quadriláteros em um papel pontilhado como o da imagem a seguir. Os pontos pretos são vértices de quadradinhos de lado \(1\,cm\) e os quadriláteros desenhados só podem usar como vértices os pontos pretos.
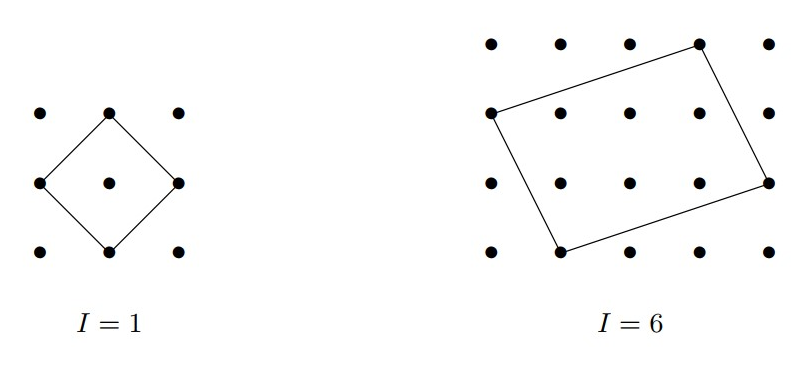
A letra \(I\) representa o número de pontos pretos no interior de cada quadrilátero.
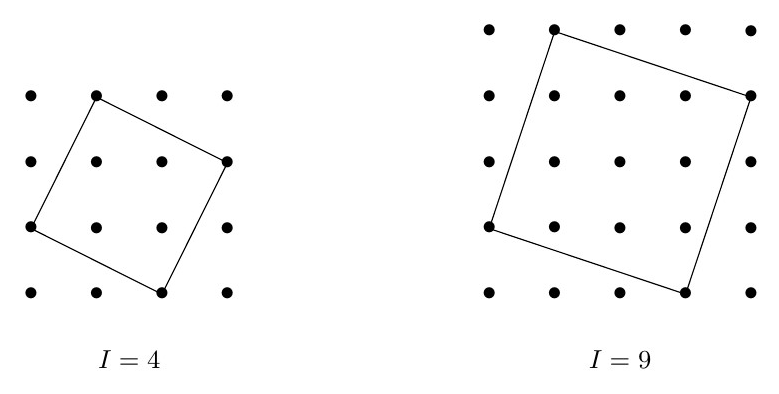
Dê exemplos, por meio de um desenho, de quadrados com \(I=4\) e \(I=9\) no papel pontilhado.
Explique como Bernardo pode desenhar losangos contendo qualquer valor de pontos interiores desejado.
Qual é a menor área possível para um triângulo com vértices nos pontos do papel?
Solução 6.
Dois quadrados, um com \(I=4\) e outro com \(I=9\):
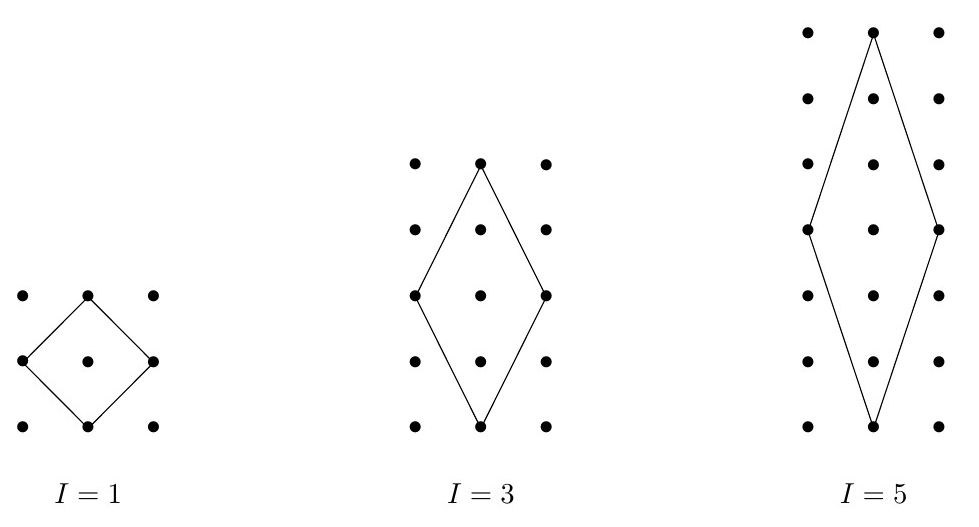
Se \(I\) é um número ímpar, podemos dispor \(I+2\) pontos consecutivos na vertical e marcar como vértices do losango os extremos dessa sequência. Os outros dois vértices são os pontos nas verticais anterior e sucessora mais próximos do centro da sequência de pontos, como indicado nas figuras a seguir:
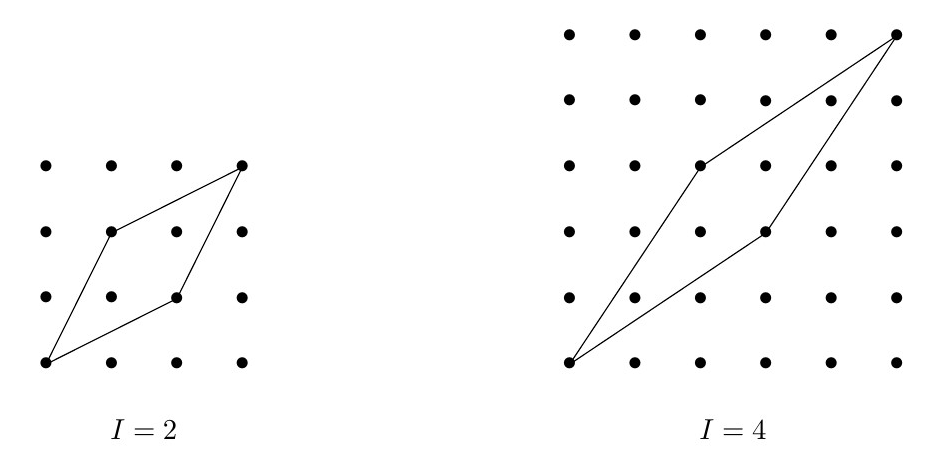
Se \(I\) é um número par, considere uma diagonal de \(I+2\) pontos consecutivos formando \(45^{\circ}\) com os lados do papel do reticulado. Os dois pontos extremos dessa diagonal serão vértices do losango. Os outros dois vértices são os \(2\) pontos mais próximos do centro da diagonal, como indicado nas figuras a seguir:
Dado qualquer triângulo com vértices nos reticulados, se dois de seus vértices estão na horizontal ou vertical (em relação aos lados do papel), a distância entre eles é um número inteiro \(b\). A altura \(h\) do terceiro vértice a esses dois também é um inteiro \(h\). A área do triângulo é, portanto,
\[\dfrac{b \cdot h}{2} \geq \dfrac{1}{2}\,\mathrm{cm}^2\]
Veja que realmente existem triângulos com área \(1/2\). Basta considerar um quadradinho \(1 \times 1\) do papel e dividi-lo ao meio por uma de suas diagonais. Veja que o argumento anterior mostra que a área de qualquer triângulo com lados paralelos aos lados da folha é da forma \(n/2\), em que \(n\) é um número inteiro. Para terminar, precisamos considerar os triângulo \(ABC\) que não possuem lados paralelos aos da folha, como na figura a seguir.
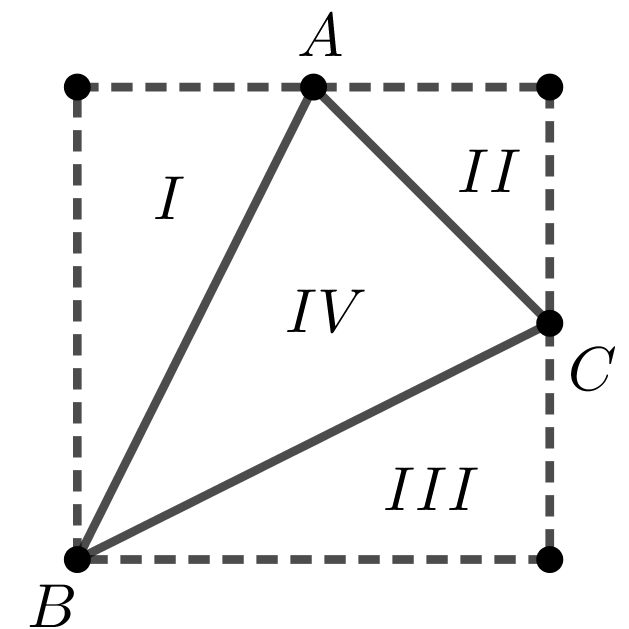
Pelos seus vértices, trace retas paralelas aos lados das folhas. As interseções dessas retas são pontos dos reticulados, e, pelo argumento anterior, podemos garantir que as áreas das regiões \(I\), \(II\) e \(III\) são números da forma \(n/2\), com \(n\) inteiro. Como a área de um retângulo com lados paralelos aos lados do tabuleiro é um número inteiro, contabilizando a diferença das áreas dos demais triângulos, podemos concluir que a área do triângulo \(IV\) ou será um número inteiro ou metade de inteiro. Em qualquer caso, o seu valor mínimo é pelo menos \(1/2\).
O Teorema de Pick permite calcular a área de qualquer polígono com vértices nos pontinhos da folha conhecendo o número de pontos interiores \(I\) e o número de pontos no bordo da figura, que será chamado de \(B\), através da fórmula:
\[A = I + \dfrac{B}{2}-1.\]
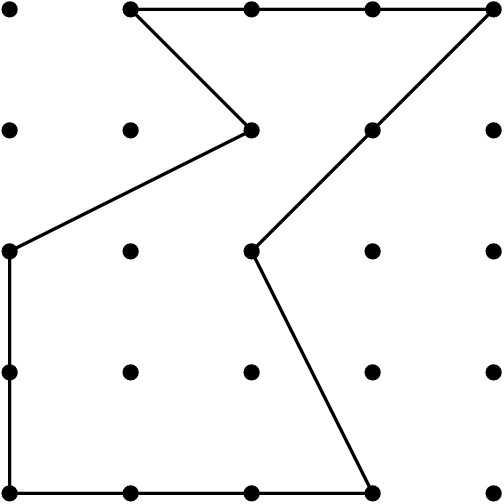
Na figura anterior, \(B=13\) e \(I=3\), e assim a área do polígono é:
\[A = 3 + \dfrac{13}{2}-1 = 8,5\,cm^2.\]
Problema 7. O número de todos os inteiros positivos de 64 dígitos sem zeros em sua representação e que são divisíveis por \(101\) é par ou ímpar?
Solução 7. Precisamos criar alguma maneira de agrupar os números em pares. Seja \(A = \underbrace{11 \ldots 11}_{64\,\,\, vezes}0\) repetições do número \(1\). Como \(1111\) é múltiplo de \(101\) é fácil ver que \(A\) é múltiplo de \(101\). Para todo número de \(64\) dígitos \(a=\overline{a_1a_2\ldots a_{63}a_{64}}\), sem zeros em sua representação decimal, considere o seu conjugado \(b = \overline{b_1b_2\ldots b_{63}b_{64}} = (10-a_1)(10-a_2) \ldots (10-a_{64})\). Nenhum dígito de \(a\) é igual a zero, portanto, cada número \(10-a_i\) pertence ao conjunto \(\{0,1,\ldots, 9\}\). Da equação \(a+b=A\) obtemos que \(a\) é divisível por \(101\) se e somente se \(b\) é divisível por \(101\)(lembre-se que \(A\) é múltiplo de \(101\)). Como o único número que é igual ao seu conjugado é o número \(\underbrace{55 \ldots 55}_{64\,\,\, vezes}\)(que é múltiplo de \(101\)) e os demais números que satisfazem o enunciado podem ser pareados, concluímos que a quantidade procurada é ímpar.
Problema 8. É possível arranjar os números \(1,1,2,2,3,3, \ldots, 1986,1986\) em fila de modo que entre quaisquer dois \(i's\) hajam \((i-1)\) números?
Solução 8. Vamos tentar fazer alguns casos pequenos. É fácil ver que não conseguimos fazer o que o enunciado pede com os números \(1,1,2,2\) mas com os números \(1,1,2,2,3,3,4,4\) temos um exemplo: \[\begin{array}{cccccccc} 1^{\circ} & 2^{\circ} & 3^{\circ} & 4^{\circ} & 5^{\circ} & 6^{\circ} & 7^{\circ} & 8^{\circ} \\ a_3 & a_4 & a_2 & b_3 & b_2 & b_4 & a_1 & b_1 \\ {\bf 3} & {\bf 4} & {\bf 2} & {\bf 3} & {\bf 2} & {\bf 4} & {\bf 1} & {\bf 1} \end{array}\] Contando da esquerda para a direita, denotemos por \(a_i\) e \(b_i\) as posições do primeiro e segundo número \(i\), respectivamente. No nosso exemplo, \(a_2 = 3\) e \(b_2 =5\). Como existem \(i-1\) números entre dois números \(i's\), devemos ter \(b_i-a_i = i\). Se é possível escrever os números \(1,1,2,2, \ldots n,n\) em linha como no enunciado, obtemos:
\[\begin{aligned} (a_1+a_2+ \ldots a_n) + (b_1+b_2+ \ldots + b_n) & = & \\ 1 + 2 + \ldots + 2n & = & n(2n+1)\\ (b_1 - a_1) + (b_2-a_2)+ \ldots (b_n-a_n) & = & \\ 1 + 2 + \ldots + n & = & \dfrac{n(n+1)}{2}. \end{aligned}\]
Somando as duas linhas,
\[\begin{aligned} 2(b_1+b_2+ \ldots b_n) = \dfrac{n(5n+3)}{2} \end{aligned}\]
Como o lado esquerdo é sempre par, a fração \(\dfrac{n(5n+3)}{2}\) deve ser um inteiro par. Isso já restringe os possíveis valores de \(n\). Para \(n=1986\),
\[\begin{aligned} \dfrac{n(5n+3)}{2} = 9863469 \end{aligned}\]
é ímpar e consequentemente não é possível dispormos esses números em linha. Uma pergunta natural que você deve tentar descobrir é, para quais \(n\), tal distribuição é possível.
Problema 9. Os alunos da \(DMAT\) aprendem \(n\) matérias no semestre. É verdade que para cada matéria exatamente 3 alunos são os melhores nessa matéria, e que para cada 2 matérias, existe exatamente um aluno que é um dos melhores nas duas. Prove que:
Se \(n=8\) existe um aluno que é um dos melhores em todas as matérias.
Se \(n=7\), não é necessário que haja um aluno que é um dos melhores em todas as matérias.
Solução 9.
Vamos inicialmente mostrar que algum aluno deve ser o melhor em \(4\) matérias. Suponha, por absurdo, que nenhum aluno é o melhor em \(4\) materias. Seja \(M_1\) uma matéria e \(\{A,B,C\}\) os três alunos que são os melhores nessa matéria. Cada um deles pode estar em no máximo mais duas matérias e qualquer outra matéria deve ter um deles. Portanto, além de \(M_1\), podem existir no máximo \(2+2+2=6\) matérias. Isso é um absurdo, pois temos mais que \(7\) matérias. Assim, existe algum aluno, que denotaremos por \(P\), que é o melhor em \(4\) matérias. Sejam \(M_1, M_2, M_3\) e \(M_4\) quatro matérias em que ele é o melhor. Vamos mostrar que \(P\) é o melhor em todas as matérias. Suponha que \(A\) não é um dos melhores alunos para a matéria \(M\). Assim, cada um dos \(3\) melhores alunos de \(M\), devem estar nos \(4\) conjuntos disjuntos: \(M_1-\{P\}\), \(M_2-\{P\}\), \(M_3-\{P\}\) e \(M_4-\{P\}\). Isso é um absurdo. Logo, \(P\) é o melhor em todas as matérias.
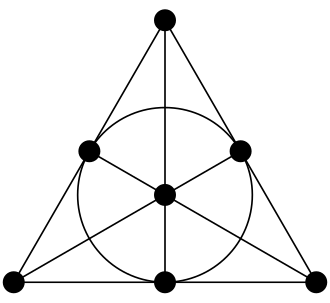
Para \(n=7\), podemos produzir um exemplo usando o diagrama de Fano da figura a seguir. Cada ponto respresenta um aluno e cada reta assim como o círculo central representam as matérias. Note que cada matéria possa por \(3\) pontos, que serão os melhores nela, e que quaisquer duas matérias possuem exatamente um ponto em comum.
Novos Problemas
Problemas Universitários
Problema 10. No plano complexo (plano de Argand-Gauss) um quadrato \(ABCD\) tem centro no ponto \(z=0\).
Se o vértice \(A\) encontra-se no afixo do número complexo \(z_1\), determine o número complexo que representa o baricentro do triângulo \(ABC\).
Problema 11. Qual o número de pares ordenados \((a,b)\) de inteiros positivos \(a, b\) tais que as seguintes condições sejam simultaneamente satisfeitas?
\(a\mid 6000\);
\(1\le b \le \frac{6000}{a}\);
\(\operatorname{mdc}(a, b,\frac{6000}{a}) = 1\).
Problema 12. Seja \(r(x)\) o polinômio que é o resto na divisão de \(x^{2050}\) por \(x^5 + x^2 +1\). Quantos coeficientes ímpares possui \(r(x)\)?
Problema 13. Considere \(\Gamma\) o lugar geométrico dos pontos \(P\) do plano cuja razão entre a distância de \(P\) à origem e a distância entre \(P\) e a reta \(y=-1\) é constante e igual a \(\frac{1}{2}\). Qual a maior distância entre dois pontos de \(\Gamma\)?
Problema 14. Seja \(f : \mathbb{R} \rightarrow \mathbb{R}\) uma função ímpar e diferenciável satisfazendo:
\(f(f(x)) = x\) para todo \(x \in \mathbb{R}\);
\(f'(0) = 1\).
Mostre que \(f(x) = -x\) para todo \(x \in \mathbb{R}\).
Problema 15. Sejam \(A, B \in M_n(\mathbb{R})\). Prove que \(\mbox{rank}(A) + \mbox{rank}(B) \leq n\) se, e somente se, existe uma matriz invertível \(X \in M_n(\mathbb{R})\) tal que \(AXB = O_n\), onde \(O_n\) é a matriz nula de ordem \(n\).
Problemas de Matemática Elementar
Problema 16. Nas Olimpíadas de Pirajuba, existem \(6\) competidores e \(8\) dias de evento. Os três primeiros competidores de cada dia do evento recebem uma medalha, que pode ser de ouro, prata e bronze. Não existem empates e uma medalhade cada tipo é dada a apenas um atleta em cada dia do evento. Cada competidor recebe \(5\) pontos por cada medalha de ouro, \(3\) pontos por cada medalha de prata e \(1\) ponto por cada medalha de bronze. Se Luciana, que é uma das competidoras, conseguiu um total de \(27\) pontos no final do evento, qual o número máximo de medalhas de prata que ela pode ter recebido?
Problema 17. Um encontro de britânicos e italianos em uma cafeteria reuniu 55 pessoas. Cada uma dessas pessoas pediu café ou chá. Sabemos que os britânicos sempre contam a verdade quando bebem chá e mentem quando bebem café. Já os italianos se comportam de modo oposto. Um repórter realizou uma rápida pesquisa e descobriu os seguintes fatos:
44 pessoas responderam “sim” para a pergunta: “Você está bebendo café?”
33 pessoas responderam “sim” para a pergunta: “Você é italiano?”
22 pessoas concordaram com a afirmação: “Está chovendo lá fora”.
Quantos britânicos na cafeteria estavam tomando chá?
Problema 18. Érica viajou para um país estrangeiro e sacou \(\$800\) da moeda local em um banco. O caixa deu essa quantia usando notas de \(\$20\), \(\$50\) e \(\$100\), usando pelo menos uma nota de cada tipo. De quantas maneiras diferentes ele pode ter feito esse pagamento para ela?
Problema 19. Na malha a seguir, todos os quadradinhos possuem lados de mesma medida. Explique o porquê de os ângulos \(\angle BAC\) e \(\angle EDF\) possuírem a mesma medida.

Problema 20. Na figura a seguir, todos os triângulos são equiláteros e idênticos. Encontre a medida do ângulo \(\angle ABC\).
Problema 21. Prove que \[\frac{1}{15} < \frac{1}{2}\cdot \frac{3}{4} \cdot \frac{5}{6} \cdots \frac{99}{100} < \frac{1}{12}\]
Problema 22. Avalie a soma simplificando ao máximo sua expressão \[\frac{2}{0! + 1! + 2!} + \frac{3}{1! + 2! + 3!} + \cdots + \frac{2024}{2022! + 2023! + 2024!}\]
Euler foi o primeiro a provar que \[\dfrac{\pi^2}{6} = \dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\ldots .\] Além dele, alguns membros da família Bernoulli, que também viviam na cidade da Basileia, tentaram obter esse resultado. Por conta disso esse resultado também ficou atrelado ao nome da cidade.↩︎
