Problema
A Basileia e outros problemas
Soluções da Edição Anterior
Problema 1. Uma malha triangular é formada pela decomposição de um triângulo equilátero de lado \(5\) em \(5^2\) triângulos equiláteros de lado \(1\), como indicado na figura. Determine o número de paralelogramos que podem ser desenhados por segmentos que formam a malha.
Solução 1 (Solução de Zezé de Oliveira). Denotemos os lados do triângulo pelas letras \(x\), \(y\) e \(z\). Qualquer paralelogramo na malha possui lados paralelos a dois dos três lados do triângulo e isso nos permite classificá-los em três tipos. Um paralelogramo tipo \(x\) possui lados paralelos aos lados \(y\) e \(z\) e assim para os demais casos. Por simetria, basta contarmos o número de paralelogramos do tipo \(x\), pois o resultado total será o triplo desse número.
Cada paralelogramo do tipo \(x\) é determinado pelas suas projeções nos lados do triângulo, que possuem comprimentos de \(1\) a \(4\). Se \(AB\) é a projeção no lado \(y\), contaremos quais os possíveis comprimentos de \(CD\), que é a projeção no lado \(z\).
Se \(AB = 4\), podemos ter apenas \(CD=1\) e assim há \(1\) paralelogramo possível.
Se \(AB = 3\), podemos ter apenas \(CD=1\) ou \(CD=2\) e assim há \[3+1=4\] paralelogramos possíveis.
Se \(AB = 2\), podemos ter apenas \(CD=1\), \(CD=2\) ou \(CD=3\) e assim há \[6+3+1=10\] paralelogramos possíveis.
Se \(AB = 1\), podemos ter apenas \(CD=1\), \(CD=2\), \(CD=3\) ou \(CD=4\) e assim há \[10+6+3+1=20\] paralelogramos possíveis.
Portanto, há \(1+4+10+20=35\) paralelogramos do tipo \(x\) e assim o total de paralelogramos na malha é \(3 \cdot 35 = 105\).
Criando uma camada extra para a malha, podemos associar de modo único cada paralelogramo do tipo \(x\) a dois segmentos disjuntos no novo lado de tamanho \(n+1\). Assim, o total de triângulos do tipo \(x\) é \({n+2 \choose 4}\) e a resposta geral é \(3 \cdot {n+2 \choose 4}\).
Problema 2. Determine a quantidade de números reais \(x\) que satisfazem a equação: \[2^{x^2+x} + \log_2 x = 2^{x+1}.\]
Solução 2 (Solução de Yure Carneiro). Por conta da função logaritmica, precisamos ter \(x > 0\). Agora vejamos os casos:
Para \(0 < x < 1,\) temos \(x^2 < 1\) e \(x^2 + x < x + 1\), de onde \[2^{x^2 + x} < 2^{x+1}\] Além disso, \(\log_2 x < 0\). Portanto, \[2^{x^2 + x} + \log_2 x < 2^{x^2 + x} < 2^{x+1}.\]
Para \(x > 1,\) temos \(x^2 > 1\) e \(x^2 + x > x + 1\), de onde \[2^{x^2 + x} > 2^{x+1}\] Além disso, \(\log_2 x > 0\). Portanto, \[2^{x^2 + x} + \log_2 x > 2^{x^2 + x} > 2^{x+1}.\]
De onde vemos que para todo \(0 < x \neq 1\), não temos verificado a igualdade \((1)\). Enquanto para \(x=1\), vale a igualdade \[2^{1^2 + 1} + \log_2 1 = 2^{1+1} + 0 = 2^{1+1}\]
De onde concluímos que existe apenas um número real \(x\) para o qual é verificado a equação dada.
Problema 3. Seja \(a\) um inteiro positivo tal que
\[1+\dfrac{1}{2}+\dfrac{1}{3}+\ldots +\dfrac{1}{25} = \dfrac{a}{25!}.\]
Encontre o resto de \(a\) na divisão por \(13\).
Solução 3 (Solução de Yure Carneiro). Veja que \[\displaystyle a = \sum_{j=1}^{25} \frac{25!}{j} \equiv \ \frac{25!}{13} \pmod{13},\] visto que as parcelas com índice \(j \neq 13\) são tais que \(13 \mid \frac{25!}{j}\). Agora temos \[\begin{aligned} a & \equiv & 1 \times 2 \times \cdots \times 12 \times 14 \times \cdots \times 25 \pmod{13}\\ & \equiv & 12! \times 1 \times 2 \times \cdots \times 12 \pmod{13}\\ & = & 12! \times 12! \end{aligned}\]
Pelo Teorema de Wilson, como \(12! = (13 -1)! \equiv -1 \pmod{13}\), segue que \[a \ \equiv \ (-1)^2 = 1 \pmod{13}\] e daí \(r=1\) é o resto de \(a\) na divisão por \(13\).
Problema 4. Um hexágono regular de lado \(1\) está inscrito na interseção de duas parábolas idênticas, mas que estão orientadas em direções opostas, i.e., uma é simétrica a outra em relação à reta que passa pelos seus pontos de interseção. Encontre a área da região sombreada, ou seja, a área que está entre as parábolas, mas que é externa ao hexágono.
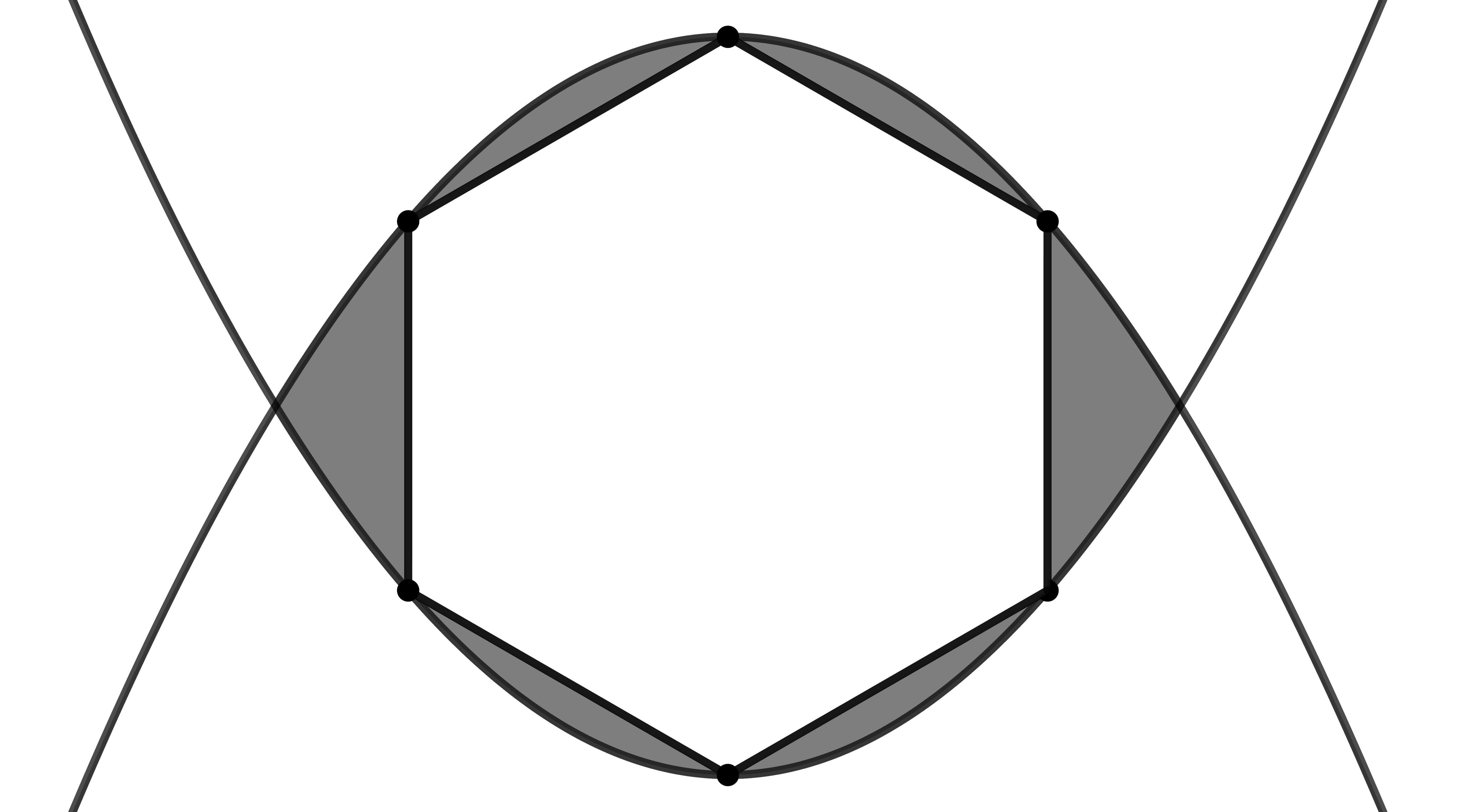
Solução 4 (Solução de Yure Carneiro). Sabemos
que a distãncia entre dois vertices opostos de um hexágono regular é
igual ao dobro da medida de seu lado. Nesse caso, essa distância é igual
a 2. Considere a situação na figura do problema e suponhamos que o
vértice da parábola de concavidade para cima (chamada aqui de parábola
1) coincide com a origem do plano \(XY\), e a reta que une os pontos de
interseção das parábolas é paralelo ao eixo \(X\).
Por conta do hexágono ali inscrito, o ponto \(\left(\frac{\sqrt{3}}{2}, \
\frac{1}{2}\right)\) está na parábola 1. Portanto, sendo \(y = ax^2\) a equação dessa parábola, vamos
ter \(\frac{1}{2} = a \cdot
(\frac{\sqrt{3}}{2})^2 = \frac{3a}{4}\), de onde \(a = \frac{2}{3}\). Assim, \(y = \frac{2x^2}{3}\) é a equação da
parábola 1. De onde segue que a parábola 2 possui equação \(y = -ax^2 + 2 = -\frac{2x^2}{3} + 2\). Além
disso a interseção entre as duas ocorre quando \(\frac{2x^2}{3} = -\frac{2x^2}{3} + 2\),
quando \(4x^2 = 6\), ou seja, \(x=-\frac{\sqrt{6}}{2}\) e \(x=\frac{\sqrt{6}}{2}\).
Assim, a área da região plana limitada pelas duas parábolas é dada por
\[\begin{aligned}
A_1 & = & \int_{-\frac{\sqrt{6}}{2}}^{\frac{\sqrt{6}}{2}}
-\frac{2x^2}{3} + 2 - \frac{2x^2}{3} \ dx \\
& = & 4 \int_{0}^{\frac{\sqrt{6}}{2}} 1 -\frac{2x^2}{3} \ dx
= 4\left(\frac{\sqrt{6}}{2}
-\frac{2\left(\frac{\sqrt{6}}{2}\right)^3}{9}\right) \\
& = & 4\left(\frac{\sqrt{6}}{2} -\frac{\sqrt{6}}{6}\right)
\\
& = & \frac{4\sqrt{6}}{3}
\end{aligned}\]
Como a área \(A_2\) do hexágono regular de lado 1 é \(A_2 = \frac{3\sqrt{3}}{2}\), segue que a área da região sombreada é \[A = A_1 - A_2 = \frac{4\sqrt{6}}{3} - \frac{3\sqrt{3}}{2} = \frac{8\sqrt{6} - 9\sqrt{3}}{6}\]
Problema 5. Calcule o valor da soma \[\displaystyle S = \sum_{k=1}^{2022} (-1)^k \cdot \dfrac{(k^2+k+1)}{k!}.\]
Solução 5 (Solução de Yure Carneiro). Testando o valor da soma para os primeiros valores de \(k\), conjectura-se que \[S_n = \sum_{k=1}^{n} (-1)^k \dfrac{(k^2 + k + 1)}{k!}\] é igual a \[-1 + \dfrac{(-1)^n \cdot (n+1)}{n!} .\]
Vamos provar essa identidade por indução:
Para \(n=1\), temos \(S_1 = (-1)^1 \dfrac{(1^2 + 1 + 1)}{1!} = -3 = -1 + \dfrac{(-1)^1 \cdot (1 + 1)}{1!}\)
Agora supomos válida a identidade para \(n\) e mostraremos que é também verificada para \(n+1\). Temos então \[{\bf HI}: \ \ S_n = -1 + \dfrac{(-1)^n \cdot (n+1)}{n!}\]
Assim, \[\begin{aligned} S_{n+1} &=& \sum_{k=1}^{n+1} (-1)^k \dfrac{(k^2 + k + 1)}{k!} \\ &= & S_n + (-1)^{n+1} \dfrac{((n+1)^2 + (n+1) + 1)}{(n+1)!}\\ &=_{ {\bf HI} } & -1 + \dfrac{(-1)^n \cdot (n+1)}{n!} \\ & +& (-1)^{n+1} \dfrac{((n+1)^2 + (n+1) + 1)}{(n+1)!} \\ &=& -1 + \dfrac{(-1)^n \cdot (n+1)^2}{(n+1)!} \\ &+& (-1)^{n+1} \dfrac{((n+1)^2 + (n+1) + 1)}{(n+1)!} \\ &=& -1 + (-1)^{n+1} \dfrac{((n+1)^2 + (n+2) - (n+1)^2)}{(n+1)!}\\ &=& -1 + (-1)^{n+1} \dfrac{(n+2)}{(n+1)!}, \end{aligned}\] como gostaríamos de demonstrar. Então a identidade é válidade para todo \(n\) inteiro positivo. Com isso,
\[S = -1 + \dfrac{(-1)^{2022} \cdot 2023}{2022!} = \dfrac{2023 - (2022!)}{2022!}\]
Problema 6. Sejam \(a\) e \(b\) números reais com \(a < b\) e sejam \(f, g : [a, b] \rightarrow (0, + \infty)\) funções contínuas tais que \(\int_{a}^b f(x) dx = \int_a^b g(x) dx\), mas \(f \neq g\). Defina \[I_n = \int_a^b \dfrac{f(x)^{n+1}}{g(x)^n} dx, \ \forall n \in \mathbb{N}\] Mostre que a sequência \((I_n)_{n \in \mathbb{N}}\) é crescente e que \(\lim_{n \rightarrow + \infty} I_n = + \infty\).
Solução 6 (Solução de Yure Carneiro). Sabendo que \(f \neq g\), que ambas são contínuas e que \(\int_{a}^b f(x) dx = \int_a^b g(x) dx\), segue que existe \(x_0 \in [a,b]\) tal que \(f(x_0) - g(x_0) = \alpha > 0\) e existe um intervalo fechado \([c,d]\) com \(c < d\) contendo \(x_0\) e contido em \([a,b]\) para o qual \(f(x) - g(x) > \frac{\alpha}{2}\) para todo \(x \in [c, d]\). Ainda nesse intervalo \[\dfrac{f(x)}{g(x)} - 1 > \dfrac{\alpha}{2g(x)}.\] Agora tomando um \(M > 0\) tal que \(0 < g(x) < M\) para todo \(x \in [a,b]\) temos \[\dfrac{f(x)}{g(x)} > 1+ \beta\] para todo \(x \in [c,d]\), onde \(\beta = \dfrac{\alpha}{2M}\).
Agora veja que \[\begin{aligned} I_{n+1} - I_n &= \int_a^b \dfrac{f(x)^{n+2}}{g(x)^{n+1}} - \dfrac{f(x)^{n+1}}{g(x)^{n}} dx \\ &= \int_a^b \dfrac{f(x)^{n+1}}{g(x)^{n+1}}[f(x) - g(x)] dx \\ &= \int_a^b \dfrac{f(x)^{n+1}}{g(x)^{n+1}}[f(x) - g(x))] dx \\ &- \int_a^b [f(x) - g(x)] dx\\ &= \int_a^b \left(\dfrac{f(x)^{n+1}}{g(x)^{n+1}} - 1 \right)[f(x) - g(x)] dx \\ &= \int_a^b \left(\dfrac{f(x)^{n+1} - g(x)^{n+1}}{g(x)^{n+1}}\right)[f(x) - g(x)] dx \\ &= \int_a^b \left(\dfrac{\sum_{k=0}^{n} f(x)^{k}g(x)^{n-k}}{g(x)^{n+1}}\right)[f(x) - g(x)]^2 dx, \end{aligned}\] Em virtude do comentário inicial, a última igualdade pode ser estimada como \[\begin{aligned} &\geq \int_c^d \left(\dfrac{\sum_{k=0}^{n} f(x)^{k}g(x)^{n-k} }{g(x)^{n+1} }\right)[f(x) - g(x)]^2 dx \\ &\geq \int_c^d \left(\dfrac{\sum_{k=0}^{n} (1+\beta)^{k}g(x)^kg(x)^{n-k} }{g(x)^{n+1} }\right)\frac{\alpha^2}{4} dx \\ &= \int_c^d \left(\dfrac{\sum_{k=0}^{n} (1+\beta)^{k}g(x)^{n} }{g(x)^{n+1} }\right)\frac{\alpha^2}{4} dx \\ &= \int_c^d \left(\dfrac{\sum_{k=0}^{n} (1+\beta)^{k} }{g(x)}\right)\frac{\alpha^2}{4} dx \\ &\geq \int_c^d \left(\dfrac{\sum_{k=0}^{n} (1+\beta)^{k} }{M}\right)\frac{\alpha^2}{4} dx\\ &= \frac{\alpha(d-c)}{2} \cdot [(1+\beta)^{n+1} - 1] \\ & >0 \end{aligned}\] De onde segue que \(I_{n+1} > I_n\) e a sequência é crescente, e além disso \[\begin{aligned} I_{n+1} &\geq \frac{\alpha(d-c)}{2} \cdot [(1+\beta)^{n+1} - 1] + I_n \\ &> \frac{\alpha(d-c)}{2} \cdot [(1+\beta)^{n+1} - 1]. \end{aligned}\]
Como \(\frac{\alpha(d-c)}{2} \cdot [(1+\beta)^{n+1} - 1] \rightarrow + \infty\) quando \(n \rightarrow + \infty\), segue que \(\displaystyle \lim_{n \rightarrow + \infty} I_n = + \infty\).
Problema 7. Na figura a seguir, \(ABCD\) e \(AEFG\) são quadrados. O segmento \(BE\) mede \(5\,cm\). Encontre a área do retângulo sombreado.
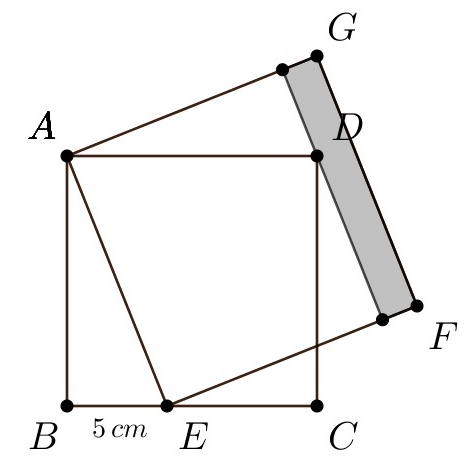
Solução 7 (Solução de Yure Carneiro). Considere a figura a seguir.
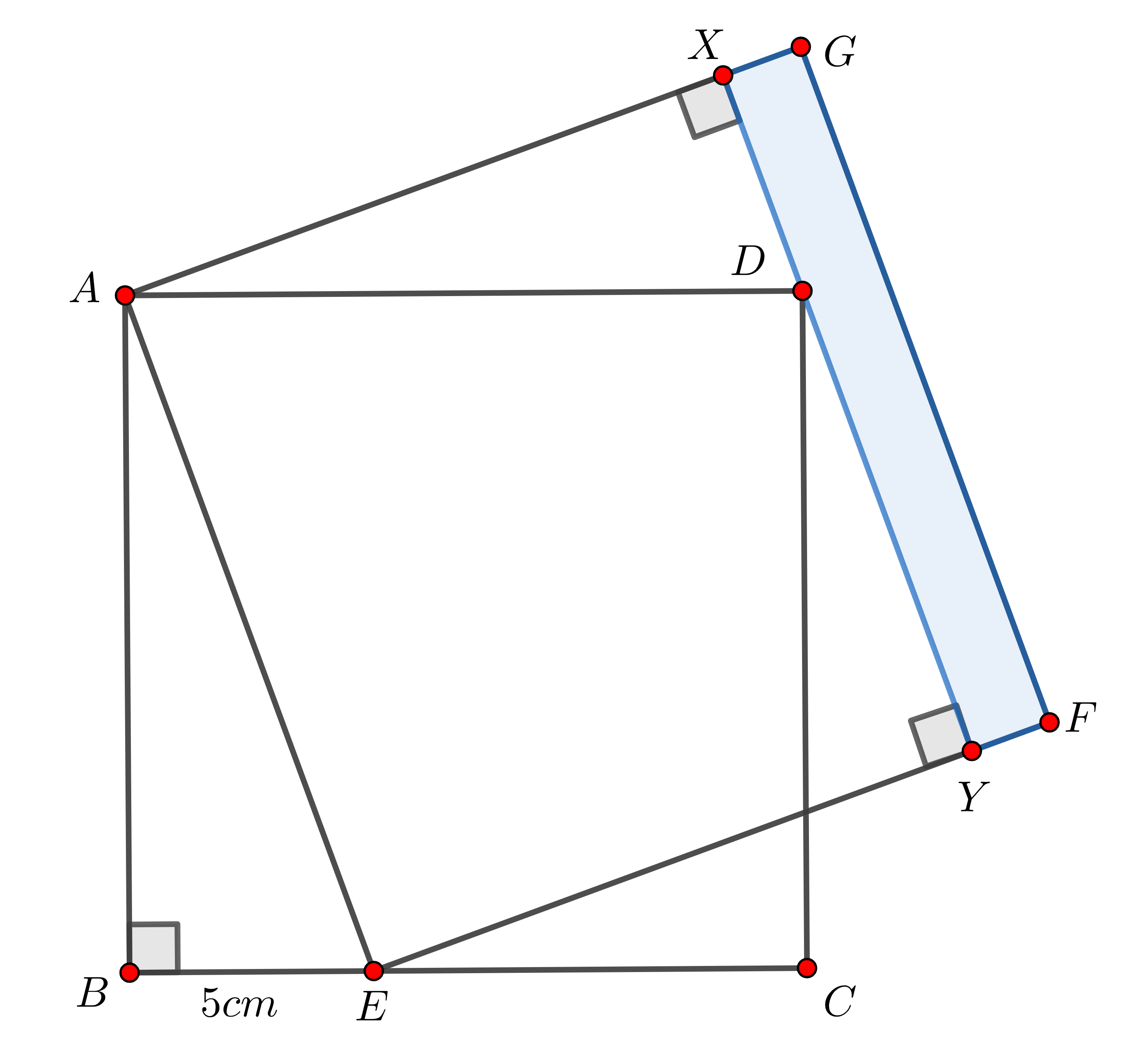
Da semelhança entre os triângulos \(ABE\) e \(AXD\), obtemos
\[\dfrac{AE}{AB} = \dfrac{AD}{AX}\] Portanto, \[AB^2 = AB \cdot AD = AE \cdot AX = [AEFG] - [XYFG] (1)\]
Além disso, do triângulo retângulo \(ABE\), temos \[AE^2 = AB^2 + BE^2 = AB^2 + 25\] \[AB^2 = AE^2 - 25\] Como \([AEFG] = AE^2\), segue das equações (1) e (2) que a aréa do retângulo sombreado é \[[XYFG] = 25 \ cm^2.\]
Problema 8. Na figura a seguir, cada quadradinho representa uma cadeira. Note que as quantidades de cadeiras consecutivas de uma mesma cor correspondem apenas aos números \(1\) e \(3\), que são ímpares.

De quantas maneiras podemos colocar \(12\) cadeiras em fila, cada uma sendo da cor branca ou cinza, de tal modo que as quantidades de cadeiras consecutivas pintadas de uma mesma cor sejam sempre números ímpares?
Solução 8 (Solução de Yure Carneiro). Considere o problema de achar o número de maneiras de obter uma soma 12 em que as parcelas são números ímpares positivos, onde a ordem das parcelas importa, ou seja, aqui consideramos que a soma \(1+1+1+9 = 12\) é uma forma de somar diferente de \(1+9+1+1 = 12\). Então a resposta ao problema das cadeiras é o dobro da resposta ao problema da soma aqui descrito. Em que cada parcela representa um conjunto de cadeiras de uma mesma cor em sequência, e podemos considerar que a primeira parcela forma um conjunto de cadeiras brancas e cada parcela na sequência está associada a uma cor entre cinza e branca que fica alternando. Exemplo: A forma de somar \(1+1+1+9 = 12\), representa a fileira de cadeiras

Já a forma de somar \(1+9+1+1 = 12\) representa a fileira

Veja que ambos começam pela cor branca. A quantidade das fileiras
que começam com a cor cinza é a mesma das que estão sendo contadas
começando com a cor branca. Assim, vamos tratar o problema das
somas.
Vamos generalizar o problema chamando de \(K_n\) o número de formas diferentes de
obter \(n\) como soma de ímpares
positivos, e onde a ordem das parcelas importa. Veja que para achar
\(K_n\) (supondo conhecidos \(K_i, \ i =1, \ldots, n-1\)) basta
considerar o seguinte, cada uma das formas de obter soma \(n\) deve começar com um dos ímpares
positivos \(j\) menores ou iguais a
\(n\), e a quantidade de maneiras de
completar a forma de somar que começa com \(j\) é exatamente igual a \(K_{n-j}\). Exemplo: para achar \(K_7\), temos as formas de obter soma \(7\) que começa com \(1, 3, 5\) e \(7\). As formas de obter soma 7 que começa
com 1 é exatamente \(K_6\). As formas
de obter soma 7 que começa com 3 é exatamente \(K_4\). As formas de obter soma 7 que começa
com 5 é exatamente \(K_2\). Já as
formas de obter soma 7 que começa com 7 é exatamente \(1\) (que denotaremos por \(K_0 = 1\)). Portanto, \[K_7 = K_6 + K_4 + K_2 + K_0\]
Generalizando, para \(n = 2j+1\) \[K_{2j+1} = K_{2j} + K_{2j-2} + \cdots + K_0 =
K_{2j} + K_{2j-1}\] e de modo análogo, para \(n = 2j\) temos \[K_{2j} = K_{2j-1} + K_{2j-3} + \cdots + K_1 =
K_{2j-1} + K_{2j-2}\]
Assim, \[K_{n} = K_{n-1} + K_{n-2}\]
Temos então que \(K_n\) é definida recursivamente pela fórmula acima, onde \(K_1 = K_0 = 1\) (ou mesmo \(K_2 = K_1 = 1\)), ou seja, \(K_n\) representa a Sequência de Fibonacci. Temos então que \(K_{12} = 144\) que é o décimo segundo termo da sequência \[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, \ldots\]
Com isso a resposta ao problema original, da quantidade de maneiras de colocar 12 cadeiras em fila conforme especificado é \[2K_{12} = 288 \ \mbox{maneiras}.\]
Problema 9. Na figura a seguir, \(X\) é um ponto no interior do triângulo equilátero \(ABC\) e \(Y\), \(W\) e \(Z\) são os pés das perpendiculares de \(X\) aos lados \(AC\), \(BC\) e \(AB\), respectivamente.
Se \(XY=k\), \(XZ=2k\), \(XW = 4k\) e a área do quadrilátero \(AYXZ\) é \(13\,cm^2\), encontre a área do triângulo \(ABC\).
Se \(XY=ak\), \(XZ=bk\) e \(XW = ck\), encontre a razão entre as áreas do triângulo \(ABC\) e do quadrilátero \(AYXZ\).
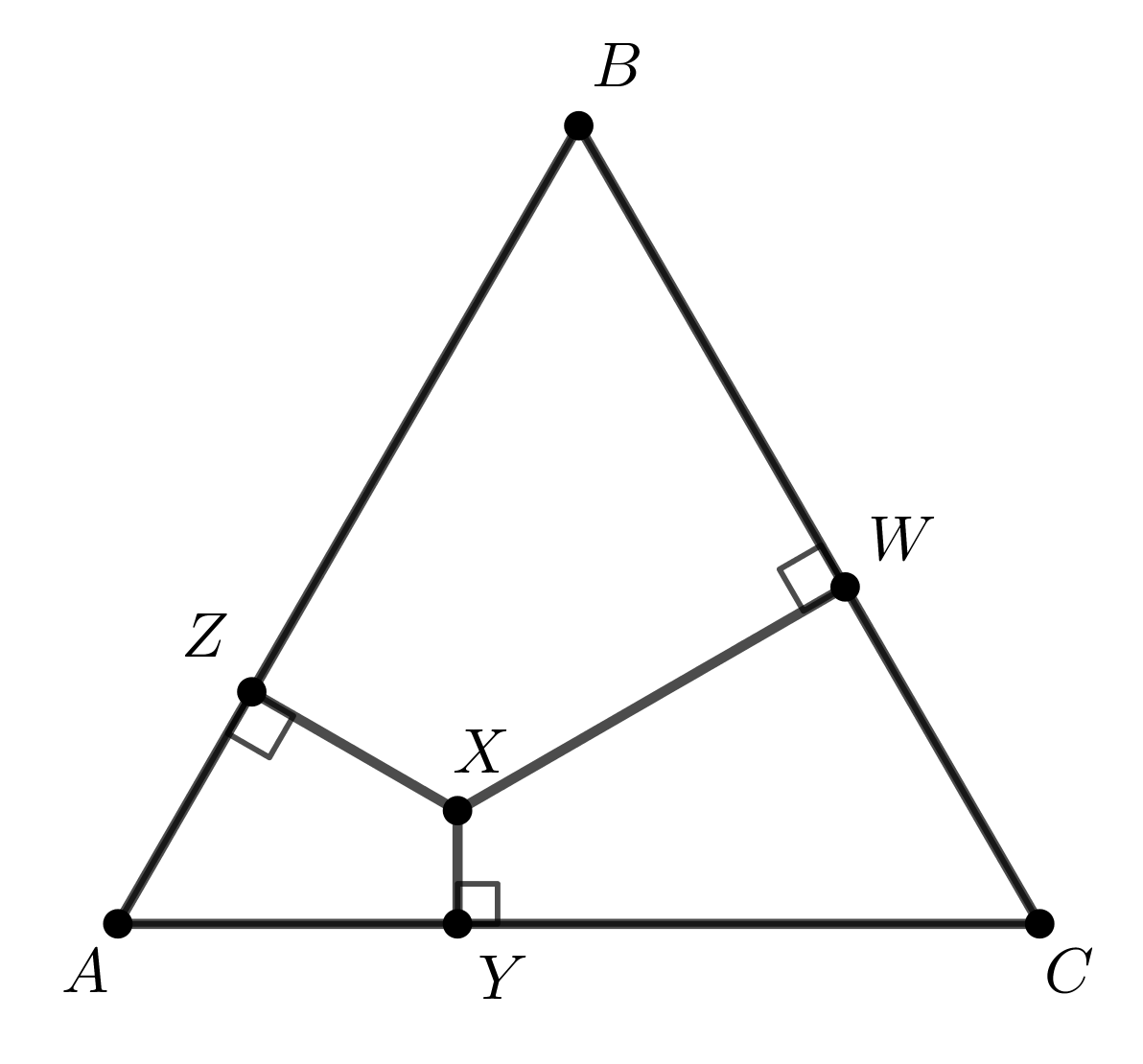
Solução 9 (Solução de Diego Alberto).
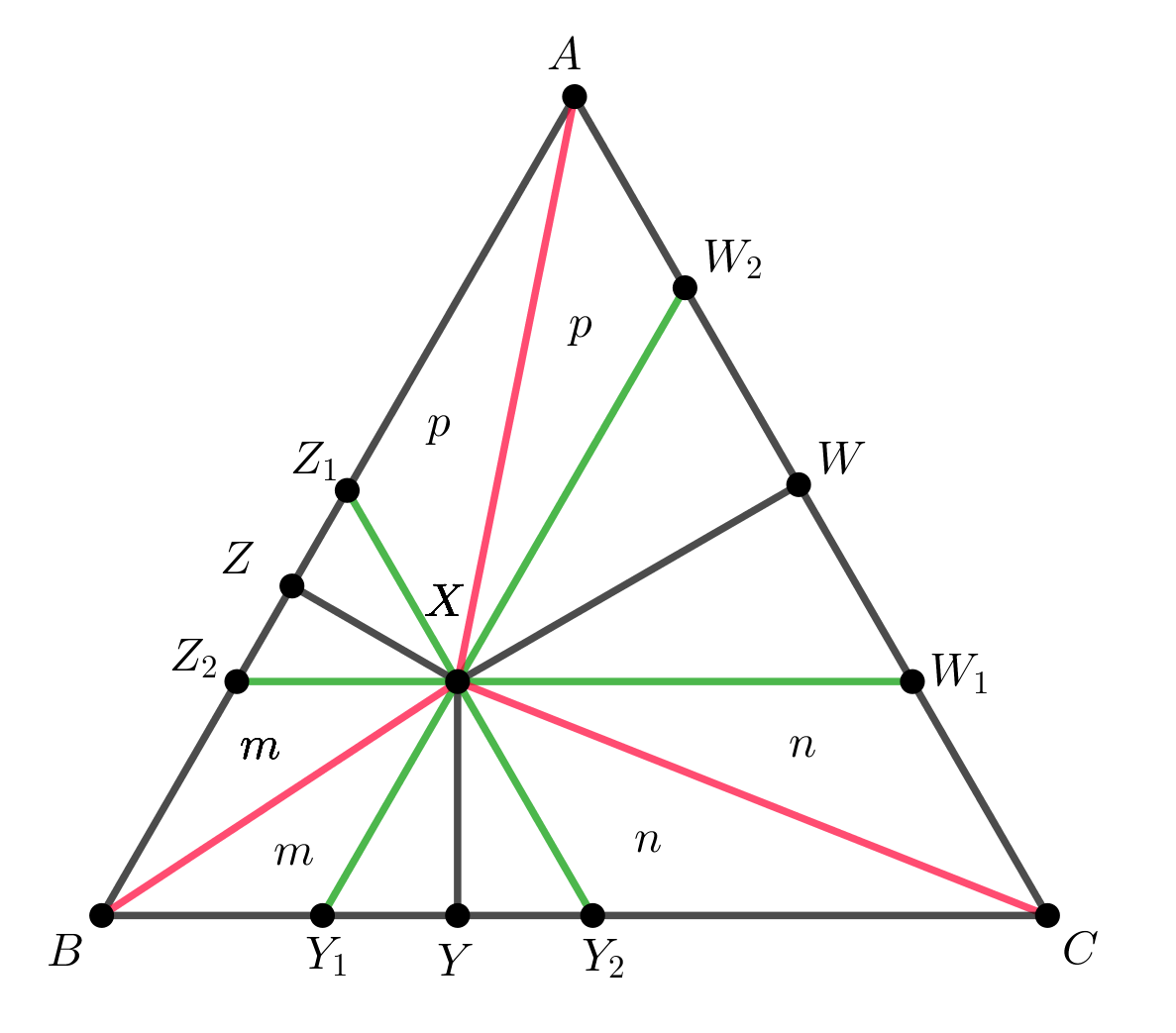
Se \(h\) é a altura do triângulo \(ABC\), temos que \[\begin{aligned} XZ \cdot AB + XY \cdot BC + XW \cdot AC & = & h \cdot AB \\ XZ + XY + XW & = & h \end{aligned}\]
Daí, \(h = 7k\). Por \(X\), trace paralelas aos lados do triângulo \(ABC\), como indicado na figura. Sejam \(S_1\), \(S_2\), \(S_3\) e \(S\) as áreas dos triângulos \(XY_1Y_2\), \(XZ_1Z_2\), \(XW_1W_2\) e \(ABC\), respectivamente. Por semelhança de triângulos, temos \[S_1/S = 4/49, S_2/S = 1/49\, \,\,\, \text{e} \,\,\, S_3/S = 16/49.\] Além disso, como os triângulos \(ABX\), \(BCX\) e \(ACX\) possuem mesma base, segue que \[A_{ABX}/S = 2/7, A_{BCX}/S = 1/7 \,\,\, \text{e} \,\,\, A_{ACX}/S = 4/7.\] Portanto, considerando as áreas representadas pelas letras \(m\), \(n\) e \(p\), temos \[\begin{aligned} m+n+S_1 & = & S/7, \\ m+p+S_2 & = & 2S/7, \\ n+p+S_3 & = & 4S/7. \end{aligned}\] Assim, \[\begin{aligned} m+n& = & 3S/49, \\ m+p& = & 13S/49, \\ n+p& = & 12S/49. \end{aligned}\] Além disso, somando todas as equações, temos \[2m+2n+2p= 28S/49.\] De \[2m+S_1/2+S_2/2=13,\] e \((4)\), obtemos \[\dfrac{5/2S}{49}-\dfrac{24S}{49} = 13 - \dfrac{28S}{49}\] e assim \(S = 98\,cm^2\)
Aproveitando a notação do item anterior, temos \(h=(a+b+c)k\) e \[\begin{aligned} m+n+S_1 & = & \dfrac{a}{(a+b+c)}S \\ m+p+S_2 & = & \dfrac{b}{(a+b+c)}S \\ n+p+S_3 & = & \dfrac{c}{(a+b+c)}S \end{aligned}\] Portanto, calculando \((5)+(6)-(7)\), temos \[2m +S_1+S_2= \dfrac{(a+b-c)S}{(a+b+c)} + \dfrac{c^2S}{(a+b+c)^2} = \dfrac{(a+b)^2S}{(a+b+c)^2}.\] \[\begin{aligned} \dfrac{S}{A_{AZXY}} & = & \dfrac{S}{2m+S_1/2+S_2/2} \\ & = & \dfrac{2S}{4m+S_1+S_2} \\ & = & \dfrac{2(a+b+c)^2}{2(a+b)^2-a^2-b^2} \\ & = & \dfrac{2(a+b+c)^2}{a^2+b^2+4ab} \end{aligned}\]
Novos Problemas
Problemas Universitários
Problema 10. Calcule o valor de \(\int_0^{\pi/2} \frac{dx}{1 + (\textrm{tg} x)^{2022}}\) é
Problema 11. Encontre o valor de
\[\displaystyle \int_0^{\pi/2} \cos^2 (\cos x)dx + \int_0^{\pi/2} \mathop{\mathrm{sen}}^2 (\mathop{\mathrm{sen}}x)dx .\]
Problema 12. Seja \(A_{2022} = (a_{ij})\) a matriz \(2022 \times 2022\) definida por
\[a_{ij} = \left \{ \begin{array}{cl} \sqrt{3}, & \text{se}\,\,i=j \\1, & \text{se}\,\,|i-j|=1 \\ 0 & \text{caso contrário} \end{array} \right .\]
Encontre o valor de \(\det A_{2022}\).
Problema 13. Sejam \(z = e^{\frac{2\pi i}{2023}} = \cos \frac{2\pi}{2023} + i\mathop{\mathrm{sen}}\frac{2\pi}{2023}\), \[A = \{1, z, z^2, \ldots, z^{2022} \}\] e \[B = \{1, 1+z, 1+z+z^2, \ldots, 1+z+z^2+ \ldots+ z^{2022} \}.\]
Determine o número de elementos de \(A \cap B\).
Problema 14. O famoso Problema da Basileia1 nos permite descobrir que
\[\dfrac{\pi^2}{8} = \dfrac{1}{1^2}+\dfrac{1}{3^2}+\dfrac{1}{5^2}+\dfrac{1}{7^2}+\ldots .\]
Vamos usar a série anterior para encontrar a soma de outra série. Para cada \(n \in \mathbb{N}\), defina como \(a_n\) seu maior divisor positivo ímpar. Por exemplo, \(a_{30} = 15\) e \(a_{24}=3\). Encontre o valor da soma:
\[S = \dfrac{a_1}{1^3}+\dfrac{a_2}{2^3}+\dfrac{a_3}{3^3}+\ldots .\]
Problemas de Matemática Elementar
Problema 15. Bernardo está brincando de desenhar quadriláteros em um papel pontilhado como o da imagem a seguir. Os pontos pretos são vértices de quadradinhos de lado \(1\,cm\) e os quadriláteros desenhados só podem usar como vértices os pontos pretos.
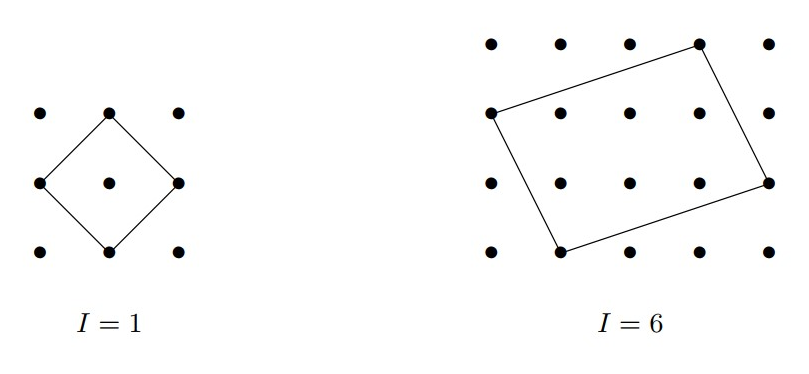
A letra \(I\) representa o número de pontos pretos no interior de cada quadrilátero.
Dê exemplos, por meio de um desenho, de quadrados com \(I=4\) e \(I=9\) no papel pontilhado.
Explique como Bernardo pode desenhar losangos contendo qualquer valor de pontos interiores desejado.
Qual é a menor área possível para um triângulo com vértices nos pontos do papel?
Problema 16. O número de todos os inteiros positivos de 64 digitos sem zeros em sua representação e que são divisíveis por \(101\) é par ou ímpar?
Problema 17. É possível arranjar os números \(1,1,2,2,3,3, \ldots, 1986,1986\) em fila de modo que entre quaisquer dois \(i's\) hajam \((i-1)\) números?
Problema 18. Os alunos da \(DMAT\) aprendem \(n\) matérias no semestre. É verdade que para cada matéria exatamente 3 alunos são os melhores nessa matéria, e que para cada 2 matérias, existe exatamente um aluno que é um dos melhores nas duas. Prove que:
Se \(n=8\) existe um aluno que é um dos melhores em todas as matérias.
Se \(n=7\), não é necessário que haja um aluno que é um dos melhores em todas as matérias.
Euler foi o primeiro a provar que \[\dfrac{\pi^2}{6} = \dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\ldots .\] Além dele, alguns membros da família Bernoulli, que também viviam na cidade da Basileia, tentaram obter esse resultado. Por conta disso esse resultado também ficou atrelado ao nome da cidade.↩︎
