Introdução

Uma das intenções de termos uma seção chamada Teorema nesta revista é permitir que o autor fale de seu resultado matemático favorito de uma maneira mais informal e pessoal do que estamos acostumados. Portanto, pedindo licença para usar a primeira pessoa, mas prometendo não abusar dessa permissão, afirmo que meu teorema favorito é o “Lema de Sperner”.

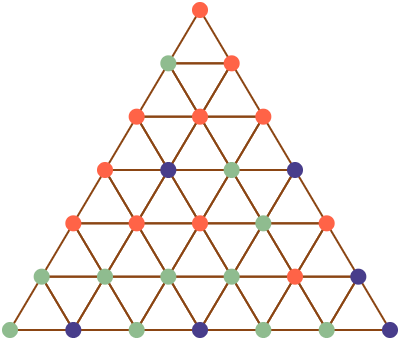
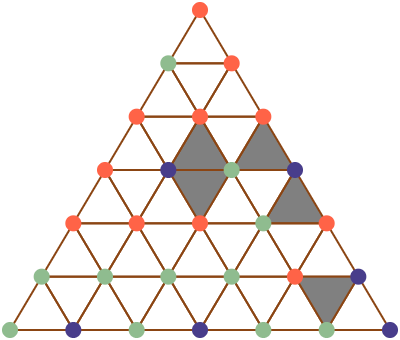
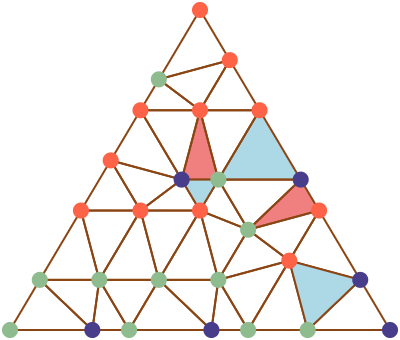
Vamos começar com um exemplo. Suponha que um dado triângulo \(\Delta = \langle v_0, v_1, v_2\rangle\) esteja triangulado, ou seja, subdividido em triângulos menores de modo que dois triângulos quaisquer ou são disjuntos, ou se intersectam em um vértice ou aresta comum, como na figura 1. Agora vamos colorir os vértices \(v_0\), \(v_1\) e \(v_2\) com três cores distintas, digamos vermelho, verde e azul, e todos os demais vértices dos triângulos menores também com as mesmas cores, de maneira arbitrária, com a única condição que os vértices interiores de uma aresta de \(\langle v_0,v_1,v_2\rangle\) não podem ter a mesma cor do vértice oposto a ela (por exemplo, os vértices sobre a aresta \(\langle v_0, v_1\rangle\) podem ter a cor de \(v_0\) ou de \(v_1\), mas não a cor de \(v_2\)). O Lema de Sperner afirma que, sob essas condições, ao menos um dos triângulos menores tem seus vértices coloridos com as três cores distintas. Destacamos na figura 2 todos os triângulos completos da figura 1, ou seja, aqueles cujos vértices estão coloridos com todas as três cores.

Meu objetivo neste artigo é contar um pouco da história deste lema de aparência tão singela, explicar por que ele é meu teorema favorito, demonstrá-lo, de mais de uma maneira, e, já que trata-se de um lema, usá-lo para esboçar a demonstração de um famoso teorema.

História

Entre 1910 e 1912, o célebre matemático holandês L.E.J. Brouwer publicou uma sequência de resultados que respondiam várias perguntas da parte da Matemática que então ainda era chamada de “Analysis Situs” (graças aos trabalhos de H. Poincaré publicados entre 1899 e 1904), mas que depois viria a se chamar Topologia. Um desses resultados é o

A demonstração desse teorema afastou de vez as preocupações geradas por certos objetos “patológicos”, tais como a curva de Peano, uma curva contínua (um objeto unidimensional) que passa por todos os pontos de um quadrado (um objeto bidimensional). O Teorema da Invariância da Dimensão mostra que não pode haver uma correspondência entre pontos de um intervalo da reta e pontos de um quadrado, por exemplo, que seja ao mesmo tempo bijetiva, contínua e com inversa contínua.

Segundo J. Dieudonné (Dieudonné 1989, 161),

…[Brouwer] usou sua descoberta [as aproximações simpliciais] para definir rigorosamente a noção de grau de uma aplicação contínua, e então prosseguiu, através das construções mais fantasticamente complicadas, baseando-se exclusivamente nesta noção, até provar os celebrados “Teoremas de Brouwer”.

Nos anos seguintes, as técnicas de Brouwer foram assimiladas até que, em 1928, Emanuel Sperner, um jovem de 23 anos de idade, provou o Teorema da Invariância da Dimensão usando o lema que leva seu nome (Sperner 1928), ou seja, com técnicas elementares, se comparadas às empregadas por Brouwer.

Vamos introduzir algumas definições para poder enunciar o Lema de Sperner¹ de maneira mais precisa. O operador de face \(\partial_i\) aplicado a um triângulo \(\Delta=\langle v_0,v_1,v_2\rangle\) obtém a aresta oposta ao \(i\)-ésimo vértice. Por exemplo, \(\partial_0 \Delta=\langle v_1, v_2\rangle\), \(\partial_1 \Delta=\langle v_0, v_2\rangle\) e \(\partial_2 \Delta=\langle v_0, v_1\rangle\). Seja \(T\) uma triangulação do triângulo \(\Delta\). Suponha que para cada vértice \(v\) de \(T\) associemos um rótulo \(L(v)\) no conjunto \(\{0,1,2\}\) (podemos usar cores nas figuras para representar esses rótulos). Dizemos que uma função de rotulação \(L\) é própria se \[v\in \partial_i\Delta \Rightarrow L(v)\neq i,\] ou seja, os vértices em uma aresta de \(\Delta\) não podem ter o mesmo rótulo do vértice oposto à aresta. Um triângulo \(\tau=\langle v_i,v_j,v_k\rangle \in T\) é completo com relação à função de rotulação \(L\) se \[\{L(v_i),L(v_j),L(v_k)\}=\{0,1,2\}\text{,}\] ou seja, os vértices de \(\tau\) possuem todos os rótulos. A versão bidimensional do Lema de Sperner que apresentamos na introdução fica assim:

Para o caso \(n=3\), teríamos uma triangulação \(T\) de um tetraedro \(\Delta\), ou seja, uma decomposição de \(\Delta\) em uma coleção de tetraedros menores que ou são disjuntos ou se intersectam em um vértice, aresta ou face comum a ambos. O operador de face funcionaria de maneira análoga, por exemplo, dado o tetraedro \(\Delta=\langle v_0,v_1,v_2,v_3\rangle\), \(\partial_2\Delta\) é a face \(\langle v_0,v_1,v_3\rangle\), e a função de rotulação associaria a cada vértice da triangulação um número no conjunto \(\{0,1,2,3\}\).

Sperner formulou seu teorema no caso geral utilizando a noção de simplexo \(n\)-dimensional ou (\(n\)-simplexo). Um \(0\)-simplexo é um ponto, \(1\)-simplexo é um segmento de reta, um \(2\)-simplexo é um triângulo, um \(3\)-simplexo é um tetraedro e assim por diante. Além disso, se observarmos a figura 2, vemos que não há apenas um triângulo completo, mas um número ímpar deles. Fazendo as devidas adaptações, chegamos assim à redação final do Lema:

Recomendo a referência (Lima 2009) para quem tiver interesse em entender melhor o enunciado geral do Lema de Sperner em termos de simplexos, mas aqui vamos nos limitar ao caso bidimensional, que é suficiente para entender o caso geral.

Um ano após a publicação do Lema de Sperner, Knaster, Kuratowski e Mazurkiewicz o aplicaram para provar outro famoso teorema de Brouwer, o

O Teorema do Ponto Fixo de Brouwer possui por si só inúmeras aplicações (Park 1999), mas mesmo assim o Lema de Sperner já foi usado para demonstrar, diretamente ou com ligeiras adaptações, vários outros teoremas importantes da Matemática, tais como o Teorema de Perron-Frobenius (Fan 1958), o Teorema Fundamental da Álgebra (Kuhn 1974) e o Teorema da Bola Cabeluda (Jarvis and Tanton 2004), além de ter encontrado aplicações interessantes na Teoria dos Jogos e na Economia (Su 1999). O ciclo se fechou quando Yoseloff mostrou em 1974 que o Lema de Sperner pode ser demonstrado por meio do Teorema do Ponto Fixo de Brouwer (Yoseloff 1974), estabelecendo-se assim uma interessante equivalência entre eles.

Devido a seu caráter elementar e pictórico e as suas variadas aplicações, o Lema de Sperner é muito popular em vídeos de divulgação matemática ((Dröge, Göttlich, and Wille 1982; Polster (Mathologer) 2017; Bazett 2018), por exemplo) e em trabalhos de conclusão de curso e dissertações de mestrado. Por exemplo, localizei duas dissertações de PROFMAT sobre o tema (Azambuja 2014; Fonseca 2017), a segunda delas orientada pelo prof. Joseph Yartey, nosso colega de departamento.

Minha história

Meu primeiro contato com o Lema de Sperner foi através do livro “A Combinatorial Introduction to Topology”, de Michael Henle (Henle 1994), ainda no começo do meu doutorado em Computação Gráfica, ou mais exatamente em Modelagem Geométrica, que é o ramo da Computação Gráfica que estuda métodos e algoritmos para a representação de formas, tais como curvas e superfícies. O objeto mais básico da Modelagem Geométrica são as malhas de triângulos, que são na verdade complexos simpliciais, como viria a aprender, e o livro de Henle contém tudo que eu precisava saber sobre o básico de topologia combinatória. Lembro de ter ficado particularmente impressionado com sua demonstração do Teorema do Ponto Fixo de Brouwer através do Lema de Sperner.

A minha tese de doutorado (Mello 2006) acabou sendo sobre subdivisão e deformação de malhas de triângulos (e de pseudovariedades combinatórias, em geral) e na parte de deformação eu tive a oportunidade de aplicar o Lema de Sperner para demonstrar uma certa propriedade (essencialmente a sobrejetividade da deformação), o que me deixou muito feliz.

Dei uma palestra sobre o Lema de Sperner no MATFEST da Universidade Federal de Alagoas em 2007 e confesso ter ficado um pouco apreensivo, pois o prof. Nicolau Saldanha, primeiro brasileiro a ganhar uma medalha de ouro na Olimpíada Internacional de Matemática e grande topologista, estava na audiência, assistindo a tudo impassível. Lá pelas tantas, eu estava jogando, contra o computador, o “Jogo de Sperner”, no qual os jogadores colocam fichas coloridas alternadamente num tabuleiro triangular e de acordo com as regras do Lema de Sperner, de modo que o perdedor é aquele que formar o primeiro triângulo completo. Jogando é forma de dizer, pois eu estava apenas clicando meio aleatoriamente nas casas, de tão nervoso. Até que em dado momento eu passei a clicar e clicar, sem que nada acontecesse. Depois de alguns longos e desconfortáveis segundos de silêncio, eu constatei que havia vencido o jogo e gritei, levantando os braços: “Ganhei!”, arrancando risadas da plateia, inclusive do prof. Nicolau, o que serviu para “quebrar o gelo”.

Demonstração

Vamos agora à demonstração mais simples do Lema. Trata-se de uma aplicação do princípio da contagem dupla, no qual contamos uma mesma quantidade de duas maneiras diferentes para chegar a um resultado.

Vamos considerar inicialmente a versão unidimensional do Lema de Sperner. Nela temos um segmento \(S\) subdividido e com os vértices coloridos com duas cores, sendo que os vértices extremos de \(S\) possuem cores diferentes, como neste exemplo:

Queremos contar o número de subsegmentos que possuem vértices de cores distintas, quantidade que denotaremos por \(\#\img[-.3em][4em][1.2em]{seggb.png}\) (no caso acima, \(\#\img[-.3em][4em][1.2em]{seggb.png}=5\) ). Para tanto, vamos contar uma outra quantidade (e aqui está o “truque” de Sperner). Seja \(F(\sigma)\) o número de vértices verdes do subsegmento \(\sigma\). Claramente, \[\begin{aligned} F(\img[-.3em][4em][1.2em]{seggg.png})&=2 \\ F(\img[-.3em][4em][1.2em]{seggb.png})&=1 \\ F(\img[-.3em][4em][1.2em]{segbg.png})&=1 \\ F(\img[-.3em][4em][1.2em]{segbb.png})&=0 . \end{aligned}\] Vamos contar \[\sum_{\sigma\in S} F(\sigma),\] ou seja, o número de vértices verdes contados por subsegmento, de duas maneiras. Por um lado, como subsegmentos da forma \(\img[-.3em][4em][1.2em]{segbb.png}\) não contribuem para o total, temos que \[\begin{equation}\label{eq:sperner1D1} \sum_{\sigma\in S} F(\sigma) = \# \img[-.3em][4em][1.2em]{seggb.png} +2\times \# \img[-.3em][4em][1.2em]{seggg.png} ,\end{equation}\] onde \(\# \img[-.3em][4em][1.2em]{seggg.png}\) denota o número de subsegmentos com os dois vértices verdes. Por outro lado, percebemos que cada vértice verde interior é contado duas vezes em \(\sum_{\sigma\in S} F(\sigma)\), já que é incidente a exatamente dois subsegmentos, ao passo que o vértice verde na fronteira de \(S\) é contado uma única vez, assim \[\begin{equation}\label{eq:sperner1D2}\begin{aligned} \sum_{\sigma\in S} F(\sigma) &= \#\left( \img[-.3em][1.2em][1.2em]{vertg.png} \text{ na fronteira}\right) \\ &+2\times \#\left( \img[-.3em][1.2em][1.2em]{vertg.png} \text{ no interior}\right). \end{aligned}\end{equation}\] Igualando as equações (\(\ref{eq:sperner1D1}\)) e (\(\ref{eq:sperner1D2}\)) e considerando a congruência módulo \(2\), temos que \[\begin{equation}\label{eq:sperner1d} \# \img[-.3em][4em][1.2em]{seggb.png} \equiv %\#\left(\vtx{1} \text{ na fronteira}\right)= 1 \pmod{2},\end{equation}\] donde concluímos que \(\# \img[-.3em][4em][1.2em]{seggb.png}\) é ímpar.

O caso bidimensional é bem parecido. Queremos contar \[\# \img[-1em][3em][3em]{trirgb.png} ,\] ou seja o número de triângulos completos. No caso da figura 2, temos que \[\# \img[-1em][3em][3em]{trirgb.png} =5.\] Seja \(F(\tau)\) o número de segmentos do tipo \(\img[-.3em][4em][1.2em]{seggb.png}\) no subtriângulo \(\tau\). Claramente, \[\begin{aligned} F\left( \img[-1em][3em][3em]{tribgb.png} \right)&=2 \\ F\left( \img[-1em][3em][3em]{triggb.png} \right)&=2 \\ F\left( \img[-1em][3em][3em]{trirgb.png} \right)&=1. \end{aligned}\] e \(F(\tau)=0\) nos demais casos. Assim, \[\begin{equation}\label{eq:sperner2d1} \sum_{\tau\in T} F(\tau) = \# \img[-1em][3em][3em]{trirgb.png} +2\times \# \img[-1em][3em][3em]{tribgb.png} +2\times \# \img[-1em][3em][3em]{triggb.png}\end{equation}\] Por outro lado, percebemos que as arestas do tipo \(\img[-.3em][4em][1.2em]{seggb.png}\) no interior de \(T\) são incidentes a exatamente dois subtriângulos, enquanto as arestas do tipo \(\img[-.3em][4em][1.2em]{seggb.png}\) na fronteira de \(T\) são incidentes a exatamente um subtriângulo, donde \[\begin{equation} \label{eq:sperner2d2} \begin{aligned} \sum_{\tau\in T} F(\tau) &= \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ na fronteira}\right) \\ &+2\times \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ no interior}\right). \end{aligned}\end{equation}\] Comparando as equações (\(\ref{eq:sperner2d1}\)) e (\(\ref{eq:sperner2d2}\)) e tomando-as módulo \(2\), temos que \[\# \img[-1em][3em][3em]{trirgb.png} \equiv \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ na fronteira}\right) \pmod{2}.\] Mas pelo caso unidimensional, ou seja, pela equação (\(\ref{eq:sperner1d}\)), concluímos que \[\# \img[-1em][3em][3em]{trirgb.png} \equiv 1 \pmod{2},\] que é exatamente a tese do Lema de Sperner, o número de triângulos completos é ímpar. Observamos também o padrão indutivo que pode ser usado para demonstrar o Lema para qualquer dimensão \(n\).

Orientação

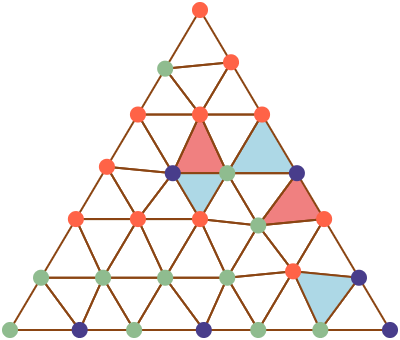
É possível refinar o resultado do Lema de Sperner usando a noção de orientação (como estabelecido em (Brown and Cairns 1961)). Na figura 3, destacamos em azul claro os triângulos completos nos quais as cores vermelho, verde e azul aparecem nesta ordem no sentido anti-horário e em vermelho claro os triângulos completos nos quais as cores vermelho, verde e azul aparecem nesta ordem no sentido horário. Podemos observar que o número de triângulos rotulados com orientação positiva (os azuis) é uma unidade a mais que os com orientação negativa (os vermelhos) (e portanto o total de triângulos completos é ímpar).

A demonstração desse fato é bem semelhante à que fizemos acima. Vamos começar com o caso unidimensional. Vamos definir \(G(\sigma)\) para um subsegmento \(\sigma\) da seguinte forma: \[\begin{aligned} G(\img[-.3em][4em][1.2em]{seggg.png} )&=1+(-1)=0 \\ G( \img[-.3em][4em][1.2em]{seggb.png} )&=1 \\ G( \img[-.3em][4em][1.2em]{segbg.png} )&=-1 \\ G( \img[-.3em][4em][1.2em]{segbb.png} )&=0 , \end{aligned}\] ou seja, \(G(\sigma)\) conta o total de vértices verdes em \(\sigma\) de acordo com sua posição: um vértice à esquerda conta \(1\) e à direita, \(-1\). Assim, \[\begin{equation}\label{eq:sperner1dori1} \sum_{\sigma\in S} G(\sigma) = \# \img[-.3em][4em][1.2em]{seggb.png} - \# \img[-.3em][4em][1.2em]{segbg.png} ,\end{equation}\] já que os segmentos \(\img[-.3em][4em][1.2em]{seggg.png}\) e \(\img[-.3em][4em][1.2em]{segbb.png}\) não contribuem para o total. Note que estamos distinguindo agora os tipos de segmentos completos \(\img[-.3em][4em][1.2em]{seggb.png}\) e \(\img[-.3em][4em][1.2em]{segbg.png}\). Por outro lado, cada vértice verde interior contribui em \(\sum_{\sigma\in S} G(\sigma)\) com \(+1\) para o segmento a sua direita e com \(-1\) para o segmento a sua esquerda, enquanto o vértice verde da fronteira de \(S\) contribui com \(1\), de modo que \[\begin{equation}\label{eq:sperner1dori2} \sum_{\sigma\in S} G(\sigma) = 1+0\times \#\left( \img[-.3em][1.2em][1.2em]{vertg.png} \text{ no interior}\right).\end{equation}\] Igualando as equações (\(\ref{eq:sperner1dori1}\)) e (\(\ref{eq:sperner1dori2}\)), concluímos que \[\begin{equation} \label{eq:sperner1dori} \# \img[-.3em][4em][1.2em]{seggb.png} - \# \img[-.3em][4em][1.2em]{segbg.png} = 1.\end{equation}\]

Vamos agora ao caso bidimensional. Seja \(G(\tau)\) quantas vezes o segmento \( \img[-.3em][4em][1.2em]{seggb.png} \) aparece na fronteira do triângulo \(\tau\), no sentido anti-horário, contando a orientação, ou seja, \[\begin{aligned} G\left( \img[-1em][3em][3em]{trirgbp.png} \right) &= 1 \\ G\left( \img[-1em][3em][3em]{trirbgn.png}\right) &= -1 \\ G\left( \img[-1em][3em][3em]{triggb.png} \right) &= 1+(-1)=0 \\ G\left( \img[-1em][3em][3em]{tribbg.png} \right) &= (-1)+1=0 \\ \end{aligned}\] etc. Assim, \[ \begin{equation}\label{eq:sperner2dori1} \begin{aligned} \sum_{\tau\in T} G(\tau) &= \# \img[-1em][3em][3em]{trirgbp.png} -\# \img[-1em][3em][3em]{trirbgn.png}\\ &+0\times \# \img[-1em][3em][3em]{tribgb.png} +0\times \# \img[-1em][3em][3em]{triggb.png} \end{aligned}\end{equation}\] Por outro lado, cada subsegmento

no interior de \(T\) contribui com sinais opostos para seus subtriângulos incidentes, donde \[ \begin{equation} \label{eq:sperner2dori2} \begin{aligned} \sum_{\tau\in T} G(\tau) &= \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ na fronteira}\right)\\[-0.4cm] &-\#\left( \img[-.3em][4em][1.2em]{segbg.png} \text{ na fronteira}\right) \\ &+0\times \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ no interior}\right). \end{aligned}\end{equation}\] Igualando as equações (\(\ref{eq:sperner2dori1}\)) e (\(\ref{eq:sperner2dori2}\)), vemos que \[\begin{aligned} \# \img[-1em][3em][3em]{trirgbp.png} -\# \img[-1em][3em][3em]{trirbgn.png} &= \#\left( \img[-.3em][4em][1.2em]{seggb.png} \text{ na fronteira}\right)\\[-0.2cm] &-\#\left( \img[-.3em][4em][1.2em]{segbg.png} \text{ na fronteira}\right) \nonumber \\ &=1, \end{aligned}\] pela equação ([eq:sperner1dori]). O padrão indutivo está claro e podemos enunciar outra versão do Lema de Sperner:

Outras Demonstrações

Várias outras demonstrações do Lema de Sperner são conhecidas. Vamos comentar algumas delas.

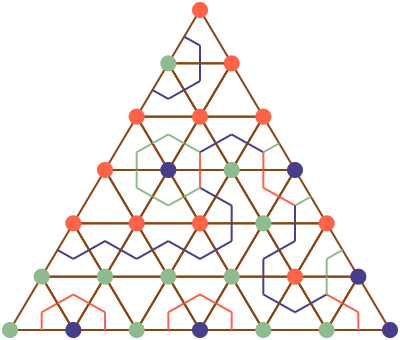
Uma demonstração bastante intuitiva envolve um certo grafo construído a partir da triangulação. Vamos pensar nos subsegmentos do tipo \(\#\img[-.3em][4em][1.2em]{segrg.png}\) como portas que dão acesso a quartos, que são os subtriângulos de \(T\) que possuem ao menos uma porta. Obviamente os quartos possuem ou duas portas (como \(\img[-1em][3em][3em]{trirgg.png}\) e \(\img[-1em][3em][3em]{trirrg.png}\) ), ou uma única porta (como \(\img[-1em][3em][3em]{trirgb.png}\) ), os quais são certamente triângulos completos. Contemple a figura 4 por um momento e veja os segmentos azuis que atravessam as portas e que representam os caminhos possíveis pelos quartos. Se entrarmos por uma das portas da fronteira, ou acabaremos voltando para o exterior do triângulo, ou chegaremos em um quarto com uma única porta (que é um triângulo completo). Mas existe um número ímpar de portas na fronteira, como já vimos, portanto certamente algum desses caminhos nos levará a um quarto sem portas e assim encontramos um triângulo completo! Por outro lado, se entrássemos em um dos quartos com uma única porta (talvez pelo telhado) e seguíssemos as portas, ou chegaríamos a uma das portas da fronteira, que são em número ímpar, ou a outro quarto com uma única porta. Assim, temos necessariamente um número ímpar de triângulos completos. Uma demonstração completa usando esse argumento pode ser vista em (Cohen 1967).

Um belo argumento “animado” envolvendo área foi descoberto recentemente (McLennan and Tourky 2008). A ideia é mover simultaneamene todos os vértices \(v_i\) da triangulação \(T\) para os vértices de mesma cor que estão nos cantos do triângulo maior (os vértices \(v_0\), \(v_1\) e \(v_2\)), ao longo de segmentos de reta. Ou seja, consideramos as triangulações \(T(t)\) que possuem as mesmas relações de incidência que \(T\) mas cujos vértices são da forma \[v_i(t) = (1-t)v_i+t v_{L(v_i)},\] com \(t\) variando continuamente no intervalo \([0,1]\). Quando \(t=0\), temos a triangulação original da figura 3. Para \(t=0.02\) e \(t=0.06\) temos as triangulações das figuras 5 e 6, respectivamente. Note como os vértices vão sendo “atraídos” para os vértices do triângulo maior de mesma cor. Seja agora \(A(t)\) a soma das áreas (com sinal) de todos os subtriângulos de \(T(t)\), onde estamos supondo que os subtriângulos de \(T(0)=T\) estejam orientados positivamente e que \(A(0)=1\). Lembro que a área com sinal de um triângulo \(\langle A,B,C\rangle\) é dada pelo determinante \[\mathop{\mathrm{Area}}\langle A,B,C\rangle= \frac{1}{2}\left|\begin{array}{ccc} 1 & 1 & 1\\ A_x & B_x & C_x \\ A_y & B_y & C_y \end{array}\right|.\] Como a triangulação é própria, os vértices sobre as arestas “deslizam” sobre elas e os vértices internos permanecem contidos no triângulo durante o movimento, de modo que \(T(t)\) é sempre uma triangulação do mesmo triângulo inicial. Também é intuitivo que a área \(A(t)\) é sempre unitária, pelo menos para \(t\) em um intervalo \([0,t_0]\), com \(t_0>0\) suficientemente pequeno, pois os vértices não têm “tempo” neste período de atravessar arestas. Mas como \(A(t)\) é um polinômio em \(t\) (verifique!), isso significa que \(A(t)\) é constante, ou seja \(A(t)=1\), para todo \(t\in[0,1]\). Vamos ver qual o valor de \(A(1)\). Ora, os subtriângulos não completos de \(T(1)\) são colapsados em vértices ou arestas, que possuem área nula. Somente os subtriângulos completos contribuem para a soma, aqueles cujos rótulos possuem orientação positiva contribuem com \(+1\), já que assumimos que o triângulo maior também possui orientação positiva, enquanto aqueles cujos rótulos possuem orientação negativa contribuem com \(-1\). E assim obtemos exatamente o resultado do caso orientado do Lema de Sperner: o número de simplexos completos com orientação positiva excede em uma unidade o número de simplexos completos com orientação negativa!

Como dissemos, Yoseloff (Yoseloff 1974) mostrou que o Lema de Sperner pode ser demonstrado usando-se o Teorema do Ponto Fixo de Brouwer. Mais exatamente, ele mostrou que se o Lema de Sperner fosse falso, seria possível construir uma aplicação contínua de um simplexo em si mesmo que não possuísse pontos fixos, o que seria uma contradição. Como estou mais interessado em argumentos elementares, não vou considerar essa classe de demonstrações indiretas aqui.

Uma outra demonstração elementar foi feita 2 anos antes da de Sperner! Isso mesmo, o Lema de Sperner é essencialmente equivalente ao Lema de Alexander, provado em 1926, história bem contada em (Ivanov 2019). Em resumo, Alexander produziu um extensa teoria sobre propriedades das aplicações simpliciais (aplicações entre complexos simpliciais que levam simplexos em simplexos) e uma delas é justamente o Lema que leva seu nome. Os lemas são equivalentes, mas há uma diferença crucial, que explica o sucesso do Lema de Sperner: o Lema de Sperner trata de rotulações dos vértices, ou seja, inteiros associados aos vértices, os quais podem ser interpretados de várias maneiras, o que torna sua aplicabilidade maior, enquanto o Lema de Alexander é sobre aplicações que levam vértices em vértices, o que é algo mais específico. Além disso, o Lema de Sperner é autocontido, enquanto o Lema de Alexander é o resultado de uma longa sequência de definições e proposições auxiliares. Recomendo a referência acima para quem tiver interesse nos detalhes. ²

“Minha Demonstração”

Não poderia terminar de falar das demonstrações do Lema de Sperner sem falar da “minha demonstração”. Não posso garantir que seja original, mas nunca a vi escrita antes. A ideia é mostrar que uma subdivisão cria ou destrói triângulos completos aos pares.

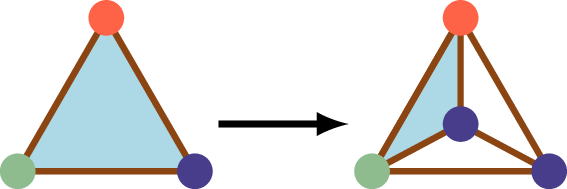
Vamos inicialmente subdividir um triângulo rotulado \(\tau\) em três subtriângulos, inserindo um vértice \(v\) em seu interior, o que chamamos de subdivisão central. Temos que considerar três casos. (i) Se \(\tau\) é completo, apenas um dos subtriângulos será completo também, qualquer que seja a cor de \(v\), uma vez que os outros dois necessariamente compartilham uma aresta com duas cores iguais:

(ii) Se \(\tau\) é quase completo, ou seja, falta apenas uma cor para ser completo, uma subdivisão central com a insercão de um vértice desta cor faltante produzirá dois subtriângulos completos:

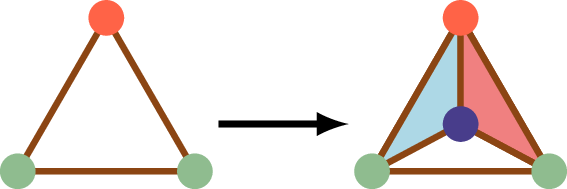
Note que neste caso os subtriângulos completos têm orientações opostas. A inserção de um vértice de outra cor não pode produzir triângulos completos. Finalmente, (iii) se \(\tau\) não é nem completo nem quase completo, a inserção de um novo vértice não pode criar triângulos completos. Assim, uma subdivisão central ou não altera o número de triângulos completos, ou aumenta o número em \(2\). Se levarmos em conta a orientação, temos que uma subdivisão central não altera a soma algébrica das orientações.

Outra subdivisão possível é uma subdivisão de uma aresta \(\epsilon\). Ao invés de considerar todos os casos possíveis, vamos implementar uma subdivisão de aresta usando subdivisões centrais e uma fusão de vértices. Temos dois casos: (i) se a aresta \(\epsilon\) for interna, para subdividi-la criando um vértice \(v\) em seu interior, vamos inicialmente aplicar uma subdivisão central em cada um dos triângulos incidentes a ela inserindo vértices \(v'\) e \(v''\) da mesma cor de \(v\):

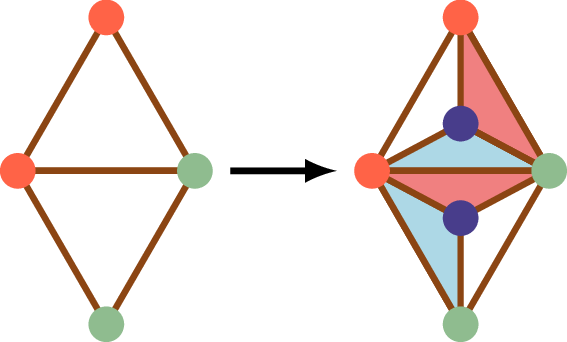
Como já vimos, isso não altera a paridade do número de triângulos completos ou a soma algébrica de suas orientações. Agora vamos “mover” os dois vértices \(v'\) e \(v''\) em direção a \(v\) para fundi-los em um único vértice:

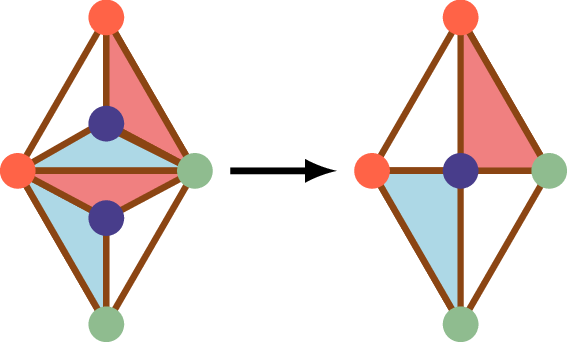
Note que a fusão dos vértices provoca o colapso dos dois triângulos incidentes a aresta \(\epsilon\), mas é claro que um deles é completo se, e somente se, o outro também é, portanto essa fusão de vértices também preserva a paridade do número de triângulos completos ou a soma algébrica de suas orientações. (ii) Se a aresta \(\epsilon\) for de fronteira, para subdividi-la inserindo um vértice \(v\) em seu interior, também efetuamos primeiro uma subdivisão central no triângulo incidente a \(\epsilon\), inserindo um vértice \(v'\) da mesma cor de \(v\):

Mas, como \(\epsilon\) é de fronteira, a cor de \(v\) (e \(v'\)) não pode ser igual a do vértice de \(\Delta\) oposto a aresta que contém \(\epsilon\), portanto o triângulo colapsado quando fundimos \(v\) e \(v'\) é necessariamente não completo:

E também a paridade do número de triângulos completos ou a soma algébrica de suas orientações é invariante.

Essas operações de subdivisão são denominadas subdivisões estelares (Lickorish 1999). No caso, estamos combinando uma subdivisão estelar com uma atribuição de rótulo (ou cor) ao vértice inserido, ou seja, estamos construindo uma função de rotulação \(L_{i+1}\) a partir de \(L_i\) à medida que subdividimos a triangulação \(T_i\) para obter a triangulação \(T_{i+1}\). Vamos chamar essa combinação de subdivisão estelar com rotulação. Dizemos que uma subdivisão estelar com rotulação aplicada a uma triangulação de um simplexo é própria se o rótulo do vértice inserido obedece as condições do Lema de Sperner, ou seja, se a função de rotulação \(L_{i+1}\) é própria sempre que \(L_{i}\) é própria. Vamos chamar de \(T_0\) a triangulação do \(n\)-simplexo \(\Delta\) que contém um único \(n\)-simplexo e \(L_0\) uma função de rotulação completa definida nos \(n+1\) vértices de \(T_0\) (portanto \(T_0\) tem um único triângulo completo). Podemos resumir o que encontramos da seguinte forma: a paridade do número de \(n\)-simplexos completos (ou a soma algébrica de suas orientações) de uma triangulação própria de um \(n\)-simplexo é invariante por subdivisões estelares próprias, donde chegamos ao seguinte

A versão estelar do Lema de Sperner pode parecer mais fraca que as outras versões que vimos, pois se aplica apenas a triangulações obtidas através de uma sequência de subdivisões estelares. Mas, em geral, esse é o caso nas aplicações do Lema de Sperner ³, com frequência usamos subdivisões baricêntricas, por exemplo, que podem ser expressas em termos de subdivisões estelares (ver figura 7).

Gosto desse argumento porque ele é quase óbvio: uma quantidade de objetos é ímpar porque ela é o resultado de um processo que, começando de um objeto, sempre acrescenta ou remove pares de objetos.

O Teorema do Ponto Fixo de Brouwer

Vamos agora esboçar brevemente a demonstração do Teorema do Ponto Fixo de Brouwer através do Lema de Sperner. Vamos considerar apenas o caso de uma aplicação contínua \(f:\Delta\rightarrow\Delta\) do triângulo \(\Delta=\langle v_0,v_1,v_2\rangle\) em si mesmo. Para poder aplicar o Lema de Sperner, precisamos atribuir um rótulo \(L(v)\in\{0,1,2\}\) aos vértices das triangulações que vamos construir. Essa atribuição fica mais simples se usarmos coordenadas baricêntricas. Cada ponto \(p\in \Delta\) pode ser localizado de maneira única pelo vetor \(w(p)=(w_0(p),w_1(p),w_2(p))\), com \[\begin{aligned} w_0(p)&=\frac{\mathop{\mathrm{Area}}\langle p,v_1,v_2\rangle} {\mathop{\mathrm{Area}}\langle v_0,v_1,v_2\rangle} \\ w_1(p)&=\frac{\mathop{\mathrm{Area}}\langle v_0,p,v_2\rangle} {\mathop{\mathrm{Area}}\langle v_0,v_1,v_2\rangle} \\ w_2(p)&=\frac{\mathop{\mathrm{Area}}\langle v_0,v_1,p\rangle} {\mathop{\mathrm{Area}}\langle v_0,v_1,v_2\rangle}, \end{aligned}\] onde claramente \(w_i\geq 0\) e \[w_0(p)+w_1(p)+w_2(p)=1.\] Também é fácil verificar que um ponto \(p\) está na aresta \(\partial_i\Delta\) se, e somente se, \(w_i(p)=0\).

Vamos definir agora a função \[g(p)=(g_0(p), g_1(p), g_2(p)),\] com \[\begin{aligned} g_0(p)&=w_0(f(p))-w_0(p) \\ g_1(p)&=w_1(f(p))-w_1(p) \\ g_2(p)&=w_2(f(p))-w_2(p). \end{aligned}\] Note que \[\begin{equation}\label{eq:barvec} g_0(p)+g_1(p)+g_2(p)=1-1=0\end{equation}\] e \(g(p)=(0,0,0)\) se, e somente se \(p=f(p)\), ou seja, se \(p\) é um ponto fixo de \(f\). Esse vetor \(g(p)\) é o vetor que liga \(p\) a \(f(p)\) expresso em coordenadas baricêntricas e que, intuitivamente, aponta para o interior, sempre que \(p\) está sobre a fronteira de \(\Delta\).

Suponha agora que \(p\) não é um ponto fixo, de modo que nem todas as coordenadas de \(g(p)\) são nulas. Pela equação (\(\ref{eq:barvec}\)), ao menos uma das coordenadas de \(g(p)\) é negativa e ao menos uma é positiva. Seja \(L(p)\) o índice da menor coordenada de \(g(p)\) (se existirem duas coordenadas iguais e negativas, seja \(L(p)\) o menor dos índices). Assim, \[g_{L(p)}(p)<0.\] Se \(p\) está na aresta \(\partial_i\Delta\), então \(w_i(p)=0\) e consequentemente \(g_i(p)=w_i(f(p))\geq 0\), que não é um valor negativo, portanto \(i\) é diferente de \(L(p)\), logo \[p\in\partial_i \Delta\Rightarrow L(p)\neq i,\] que é a condição para uma rotulação ser própria.

Se \(p\) é um ponto fixo, por acaso, atribuímos a \(L(p)\) um índice arbitrário que garanta que a rotulação seja própria. Por exemplo, podemos fazer \(L(p)=0\) se \(p\notin\partial_0\Delta\) e \(L(p)=1\), caso contrário.

Em qualquer dos casos, temos que a função de rotulação \(L\) satisfaz \[\begin{equation}\label{eq:cond} g_{L(p)}(p)\leq 0.\end{equation}\]

Vamos construir agora uma sequência \(T_i\) de triangulações de \(\Delta\) que vão ficando cada vez mais refinadas à medida que \(i\) cresce, ou seja, \(T_i\) é tal que o diâmetro do subtriângulo de maior diâmetro de \(T_i\) tende a zero quando \(i\) tende a infinito. Podemos obter essa sequência tomando sucessivas subdivisões baricêntricas do triângulo \(\Delta\), por exemplo.

Rotulando os vértices de cada \(T_i\) com a função \(L\) e aplicando o Lema de Sperner, obtemos uma sequência de triângulos completos \(\tau_i\in T_i\) cujos diâmetros tendem a zero quando \(i\) tende a infinito. Façamos \(p_{j,i}\) o vértice de \(\tau_i\) rotulado com o índice \(j\) (assim, \(L(p_{j,i})=j\)) e \(p_i\) o baricentro de \(\tau_i\), ou seja, \[p_i=\frac{p_{0,i}+p_{1,i}+p_{2,i}}{3}.\]

Como \(\Delta\) é um conjunto compacto, \(p_i\) possui uma subsequência convergente, de modo que, passando a uma subsequência de \(p_i\) se necessário, podemos assumir que \(p_i\) converge para um certo ponto \(p\).

Vamos mostrar que este ponto \(p\) é um ponto fixo de \(f\). Como o diâmetro de \(\tau_i\) tende a zero, isso significa que seus vértices \(p_{j,i}\) também convergem para \(p\). Ora, como \(g\) é uma função contínua, segue que \(g(p_{j,i})\) converge para \(g(p)\). Mas pela equação (\(\ref{eq:cond}\)), \(g_j(p_{j,i})\leq 0\), portanto \(g_j(p)\leq 0\) e pela equação (\(\ref{eq:barvec}\)), a única chance disso ocorrer é se \(g(p)=(0,0,0)\), logo \(p\) é um ponto fixo.

Esse argumento é uma adaptação do que li no livro de M. Henle citado acima. Mas é possível demonstrar o Teorema de Brouwer usando o Lema de Sperner também usando a ideia de retração (Huang 2004) ou a ideia de cobertura de fechados (Aleksandrov 1956), que foi o método usado por Knaster, Kuratowski e Mazurkiewicz na década de \(20\), o que mostra mais uma vez a flexibilidade do Lema de Sperner.

Conclusão

Acho que ficou claro o quanto gosto do Lema de Sperner. Espero que este artigo sirva para despertar o interesse pelo “Meu Teorema Favorito” e pela Matemática em geral nas novas gerações. Algumas das figuras exibidas neste artigo foram geradas manipulando um site interativo que desenvolvi e que está diponível em https://observablehq.com/@vinicius-mello/sperners-lemma.

Vinícius Mello nasceu em Salvador e obteve seu doutorado em Computação Gráfica no IMPA. Ensina matemática na UFBA e fica alegre sempre que pode usar o GeoGebra em suas aulas. Gosta de matemática, música e programação em exata proporção, podendo ser encontrado a (quase) qualquer momento fazendo ao menos uma dessas coisas.

Bibliografia