Técnica

Números Complexos e Combinatória

Samuel Feitosa

Um problema de motivação

O leitor já deve ter se deparado alguma vez com problemas recreativos, mais popularmente conhecidos como Puzzles ou Quebra-cabeças, que contêm alguma pergunta divertida cuja solução depende de algum argumento matemático ou do emprego de alguma Técnica inusitada. Esse é o propósito do exercício a seguir.

Exercício 1. Um triminó é um retângulo $3 \times 1$. Um monominó é um único quadrado $1 \times 1$. Quais as possíveis posições de um monominó em uma cobertura de um tabuleiro $8 \times 8$ usando 21 triminós e 1 monominó?

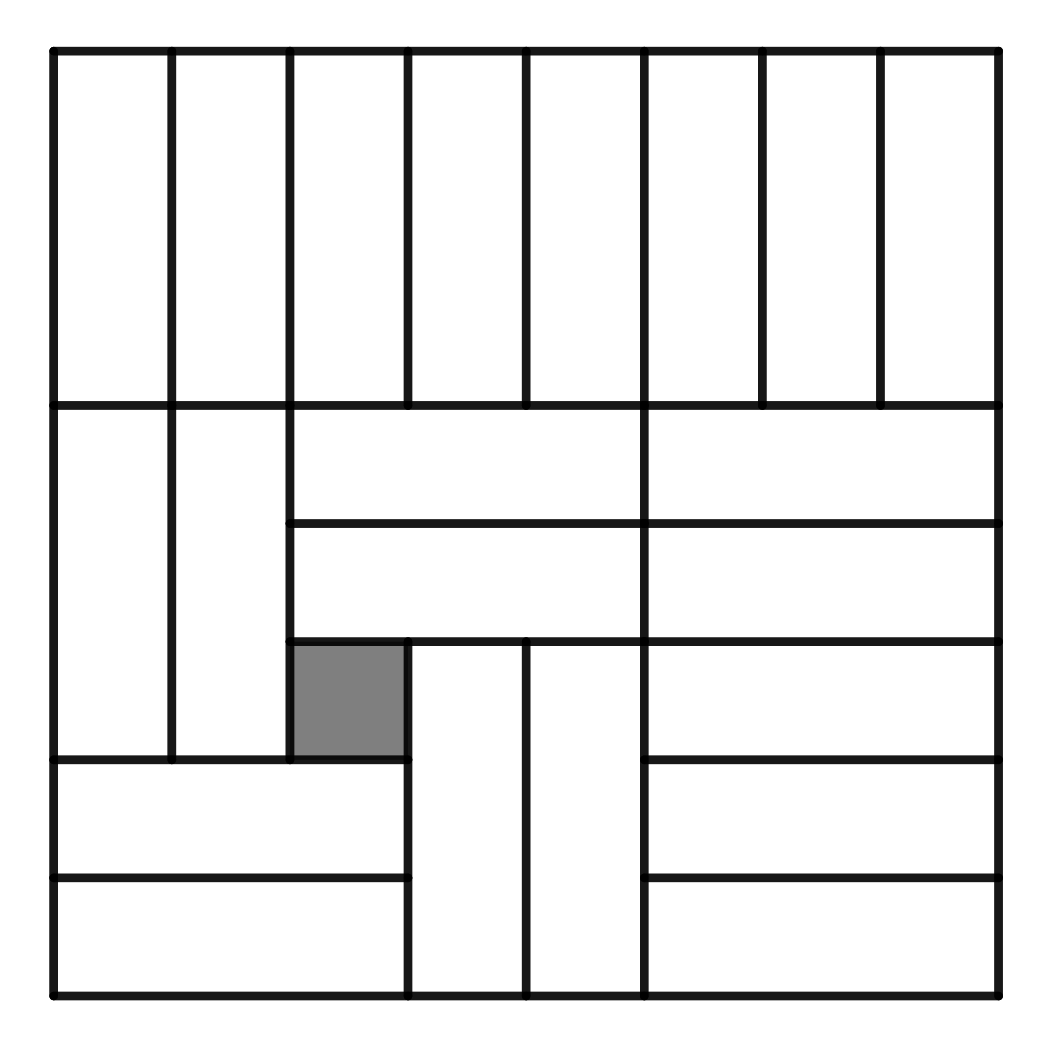
Convidamos o leitor a tentar resolvê-lo antes de continuar a ler nas próximas linhas a solução (inesperada) que envolverá números complexos.

Preliminares

Dado um $n$ inteiro positivo, uma raiz $n$-ésima da unidade é qualquer número complexo $w$ que satisfaz a equação

\[\label{eq:complexos} x^n =1.\]

Um desses números é $w = \textrm{cos} \dfrac{2\pi}{n} + i \textrm{sen} \dfrac{2\pi}{n}$ e qualquer outro que também satisfaz a equação é uma de suas potências:

\[w^2, w^3, w^4, \ldots\]

Essas potências são os vértices de um polígono regular de $n$ lados com centro na origem. Existe uma estrutura algébrica atrelada às raízes de ([eq:complexos]) que cria uma importante conexão com fenômenos de contagem. A primeira parte dessa estrutura é que o produto de quaisquer duas raízes também é uma raiz. De fato, se $x_1^n=1$ e $x_2^n=1$, então $(x_1x_2)^n=1$. A segunda parte é que o inverso de uma raiz também é uma raiz, pois se $x^n=1$ então $(1/x)^n =1$. A tabela a seguir é um exemplo de tabuada multiplicativa das raízes cúbicas da unidade, i.e., das raízes de $x^3=1$. Note que $w^3=w^0=1$.

$\times$	$w^0$	$w^1$	$w^2$
$w^0$	$w^0$	$w^1$	$w^2$
$w^1$	$w^1$	$w^2$	$w^0$
$w^2$	$w^2$	$w^0$	$w^1$

Vejamos um exercício envolvendo uma raiz quarta da unidade e números binomiais.

Exercício 2. (ITA) Para cada $n$, temos que \[1 - {4n \choose 2} + {4n \choose 4}-\ldots - {4n \choose 4n-2}+1\] é igual a:
a) $(-1)^n \cdot 2^{2n}$ b) $2^{2n}$ c) $(-1)^n \cdot 2^{n}$
d) $(-1)^{n+1} \cdot 2^{2n}$ e) $(-1)^{n+1} \cdot 2^{n}$.

Solução 1. Para calcular a soma dos números binomiais de índices pares ou ímpares, é conhecido o uso da soma $(1+1)^n+(1-1)^n$. Como $i^2=-1$, para encontrar a soma alternada descrita no problema, calculemos \[\begin{aligned} (i+1)^{4n} & = & \sum_{k=0}^{4n} {4n \choose k } i^k \\ ((i+1)^2)^{2n} & = & \sum_{j=0}^{2n} {4n \choose 2j } i^{2j} \\ & + & \sum_{j=0}^{2n-1} {4n \choose 2j+1 } i^{2j+1} \\ (2i)^{2n} & = & \sum_{j=0}^{2n} {4n \choose 2j } (-1)^j \\ & + & i\left ( \sum_{j=0}^{2n-1} {4n \choose 2j+1 } (-1)^j \right ). \end{aligned}\] Como $(2i)^{2n} = (-1)^n2^{2n}$ é número real, podemos concluir que \[\begin{aligned} \sum_{j=0}^{2n} {4n \choose 2j } (-1)^j & = & (-1)^n2^{2n} \,\,\, \text{e}\\ \sum_{j=0}^{2n-1} {4n \choose 2j+1 } (-1)^j & = & 0. \end{aligned}\] A resposta é a letra $A$.

Outra propriedade relevante sobre raízes $n$-ésimas da unidade é que a soma de todas elas é sempre zero. Para verificar isso, se $w = \textrm{cos} \dfrac{2\pi}{n} + i \textrm{sen} \dfrac{2\pi}{n}$, então $w^n-1=0$ e daí \[(w-1)(w^{n-1}+w^{n-2}+\ldots w+1) = 0.\]

Como $w \neq 1$, temos \[w^{n-1}+w^{n-2}+\ldots w+1 = 0.\]

De forma mais geral, se $n \nmid k$, como $w^k \neq 1$, temos

\[\begin{aligned} w^{k(n-1)}+w^{k(n-2)}+\ldots w^k+1 & = & \dfrac{w^{nk}-1}{w^k-1} \\ & = & \dfrac{1-1}{w^k -1} \\ & = & 0. \end{aligned}\]

Agora, vejamos uma aplicação real em um problema de combinatória. É possível cobrirmos um tabuleiro $6 \times 10$ com peças $1\times 4$, que podem ser colocadas na vertical ou horizontal sem sobreposição?

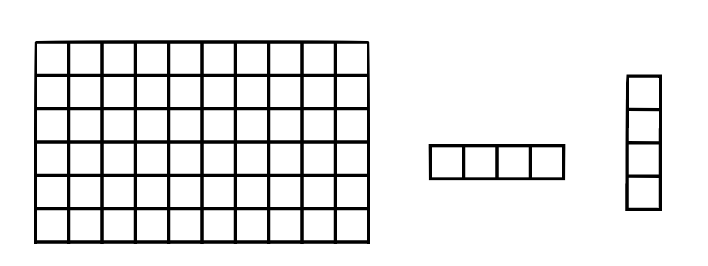
Uma abordagem natural é contar o total de quadradinhos do tabuleiro, que é $6 \cdot 10 = 60$, e notar que ele é múltiplo de $4$. Assim, precisaríamos de $60/4=15$ peças $1 \times 4$ para cobrir. Infelizmente, apenas essa condição não é suficiente. Por exemplo, apesar de um tabuleiro $2 \times 2$ ter uma quantidade de quadradinhos múltiplo de $4$, claramente não podemos cobri-lo com peças $1 \times 4$. Por outro lado, se uma das dimensões do tabuleiro for múltiplo de $4$, é fácil imaginar uma cobertura: basta cobrir esse lado com peças enfileiradas e repetir essa configuração nas demais linhas ou colunas.

O próximo teorema responde essa pergunta em geral.

Teorema 1. (Klarner) Sejam $m,n,p$ inteiros positivos dados. Se podemos cobrir um tabuleiro $m\times n$ usando peças $1\times p$, sem sobras ou superposições de peças, então $p$ divide $m$ ou $p$ divide $n$.

Proof. Suponha que podemos cobrir o tabuleiro como se pede. Para que a peça caiba no tabuleiro, devemos ter $p\leq\max\{m,n\}$. Particione o tabuleiro em $m$ linhas $1\times n$ e $n$ colunas $1\times m$, numerando as linhas do mesmo de cima para baixo, de $1$ a $m$, e as colunas da esquerda para a direita, de $1$ a $n$ (como em uma matriz $m\times n$). Em seguida escreva, na casa $ij$ do tabuleiro, o número complexo $w^{i+j}$, em que $w=\,\mbox{$\rm{cis}\,$}\frac{2\pi}{p}$. A soma de todos os números escritos na linha $i$ é

\[\begin{aligned} w^{i+1}+w^{i+2}+\ldots +w^{i+n} & = & w^i(w+w^2+\ldots +w^n) \\ & = & w^{i+1} \cdot \dfrac{w^n-1}{w-1}. \end{aligned}\]

Somando agora para todas as linhas, podemos concluir que a soma dos números no tabuleiro é

\[\begin{aligned} \displaystyle \sum_{i=1}^{m} w^{i+1} \cdot \dfrac{w^n-1}{w-1} & = & w^2 \cdot \dfrac{w^n-1}{w-1} \cdot \dfrac{w^m-1}{w-1}. \end{aligned}\]

Vamos calcular essa soma agora de outra maneira. Considere uma peça $1 \times p$ na horizontal ocupando as casas de entradas:

\[(i\,j), (i+1\, j), (i+2\, j) \ldots (i+p-1\, j).\]

A soma dos números correspondentes a essas casas é

\[\begin{aligned} w^{i+j}+w^{i+1+j}+w^{i+2+j}+\ldots w^{i+p-1+j} & = & \\ w^{i+j} \cdot (1+w+\ldots +w^{p-1}) & = & \\ w^{i+j} \cdot \dfrac{w^p-1}{w-1} & = & \\ & = & 0. \end{aligned}\]

O mesmo argumento se aplica quando a peça está na vertical. Assim, como o tabuleiro pode ser coberto, agrupando os números das casas pertencentes a uma mesma peça, podemos concluir que a soma total dos números do tabuleiro é $0$. Ou seja,

\[w^2 \cdot \dfrac{w^n-1}{w-1} \cdot \dfrac{w^m-1}{w-1} = 0.\]

Para que isso ocorra, devemos ter $w^n-1=0$ ou $w^m-1=0$ e assim $p \mid n$ ou $p \mid m$. Para verificar que é sempre possível cobrir o tabuleiro quando uma de suas dimensões é divisível por $p$, basta imitar a figura anterior. ◻

O próximo exercício é uma aplicação direta das ideias da demonstração anterior

Exercício 3. (Olimpíada Russa) Encontre o menor inteiro $n$ tal que um tabuleiro $n \times n$ pode ser particionado em subtabuleiros $40 \times 40$ e $49 \times 49$ de modo que ambos os tipos de quadrados estejam presentes na partição.

Solução 2. Assim como na solução anterior, vamos considerar uma numeração para as linhas e colunas do tabuleiro como em uma matriz $n \times n$ e associar a cada quadradinho $(ij)$ o número complexo $w^i\xi^j$, em que $w =\,\mbox{$\rm{cis}\,$}\frac{2\pi}{40}$ e $\xi = \,\mbox{$\rm{cis}\,$}\frac{2\pi}{49}$. A soma total dos números escritos no tabuleiro é \[\begin{aligned} (w^1+w^2+\ldots +w^n)(\xi^1+\xi^2+\ldots +\xi^n) & = & \\ \dfrac{w(w^n-1)}{w-1} \cdot \dfrac{\xi(\xi^n-1)}{\xi -1}. && \end{aligned}\]

De modo semelhante, se $(ij)$ é o quadradinho do canto superior esquerdo de um quadrado $k \times k$, então a soma de todos os números em seus quadradinhos é

\[\begin{aligned} (w^{i}+w^{i+1}+\ldots +w^{i+k-1})(\xi^j+\xi^{j+1}+\ldots +\xi^{j+k-1}) & = & \\ \dfrac{w^i(w^k-1)}{w-1} \cdot \dfrac{\xi^j(\xi^k-1)}{\xi -1} & = & \\ 0, && \end{aligned}\] pois se $k=40$, então $w^k-1=0$ e se $k=49$ então $\xi^k-1=0$. Portanto, caso seja possível tabuleiro com tais quadrados, a soma de todos os números escritos deve ser $0$ e daí

\[\dfrac{w(w^n-1)}{w-1} \cdot \dfrac{\xi(\xi^n-1}{\xi -1} = 0.\]

Se $w^n-1=0$ temos $40 \mid n$ e se $\xi^n-1=0$ temos $49 \mid n$. Para tratar desses dois casos, sejam $a$ e $b$ as quantidades de quadrados de tamanhos $40 \times 40$ e $49 \times 49$ usados na cobertura, respectivamente. Assim, considerando o total de quadrados cobertos, temos

\[n^2 = a \cdot 40^2+b \cdot 49^2.\]

Se $40 \mid n$, temos que $40^2 \mid b \cdot 49^2$, e como $mdc(40,49)=1$, segue que $40^2 \mid b$. Assim, como $a$ e $b$ são positivos, podemos estimar

\[\begin{aligned} n^2 & = & a \cdot 40^2+b \cdot 49^2 \\ & > & 40^2 \cdot 49^2 \\ & = & (40\cdot 49)^2. \end{aligned}\]

Daí, $n$ é pelo menos $40 \cdot 50 =2000$. Para mostrar que é possível cobrir um tabuleiro $2000 \times 2000$ com tais peças, cubra a borda esquerda e superior com quadrados $40 \times 40$ como na figura a seguir.

Para cobrir o restante da região, que é um quadrado de lado $1960 = 40 \cdot 49$, crie $40$ linhas e $40$ colunas com espaçamento de $49$ quadradinhos e cubra com $40^2$ quadrados de lado $49$.
Se $49 \mid n$, de modo semelhante ao caso anterior, $49^2 \mid a$ e daí $n \geq 49 \cdot 41 = 2009 >2000$.

Considerando ambos os casos, o menor valor possível para $n$ é $2000$.

O próximo exercício ilustra a técnica de associarmos funções geradoras a problemas de contagem.

Exercício 4. (Olimpíada Chinesa) Encontre o número de subconjuntos de $\{1,2,3 \ldots, 2000\}$ tais que a soma dos elementos é divisível por $5$.

Solução 3. Antes de resolver o exercício proposto, considere um enunciado mais simples em que queremos apenas contar quantos subconjuntos de $\{1,2,3\}$ possuem soma de seus elementos igual a $3$. Um solução seria listar explicitamente todos os $8$ subconjuntos e calcular para cada um deles a soma de seus elementos: \[\begin{aligned} \emptyset & \rightarrow & 0 \\ \{1\} & \rightarrow & 1 \\ \{2\} & \rightarrow & 2 \\ \{3\} & \rightarrow & 3 \\ \{1,2\} & \rightarrow & 3 \\ \{1,3\} & \rightarrow & 4 \\ \{2,3\} & \rightarrow & 5 \\ \{1,2,3\} & \rightarrow & 6 \\ \end{aligned}\]

Considere agora o polinômio

\[\begin{aligned} p_3(x) & = & (1+x)(1+x^2)(1+x^3) \\ & = & x^6+x^5+x^4+2x^3+x^2+x+1. \end{aligned}\]

Para obter a expressão da última linha, utilizamos a propriedade distributiva. Note que cada monômio de $p_3(x)$ pode ser associado a um subjunto de $\{1,2,3\}$. Por exemplo, o monômio $x^4$ surge através do produto $x^1 \cdot 1 \cdot x^3$, que pode ser interpretado da seguinte forma: no primeiro parênteses escolhemos $x^1$, no segundo não escolhemos $x^2$ e no terceiro escolhemos $x^3$. Essas escolhas podem ser associadas ao subconjunto $\{1,3\}$. Note que, associadas ao mesmo monômio $x^3$, existem duas escolhas de subconjunto: $x^1 \cdot x^2 \cdot 1$ e $1 \cdot 1 \cdot x^3$. Por isso o seu coeficiente na expressão que determina $p_3(x)$ é $2$. É possível fazer uma correspondência biunívoca entre as somas de elementos de subconjuntos de $\{1,2,3, \ldots, n\}$ que valem $k$ e os monômios $x^k$ que aparecem no desenvolvimento de

\[p_n(x) = (1+x)(1+x^2) \ldots (1+x^n).\]

Assim, para resolver o problema, basta somarmos todos os coeficientes dos monômios $x^k$ em $p_{2000}(x)$ quando $k$ é um múltiplo de $5$. Para calcular essa soma vamos precisar das raízes quintas da unidade! Seja $w =\,\mbox{$\rm{cis}\,$}\frac{2\pi}{5}$. Como $w$, $w^2$, $w^3$ e $w^4$ são as raízes de $1+x+x^2+x^3+x^4=0$, segue que \[1+x+x^2+x^3+x^4 = (x-w)(x-w^2)(x-w^3)(x-w^4).\\ \]

Substituindo $x=-1$, temos \[1 = (1+w)(1+w^2)(1+w^3)(1+w^4).\] Portanto, \[\begin{aligned} \prod_{j=1}^{5}(1+w^{5k+j}) & = & \\ (1+w)(1+w^2)(1+w^3)(1+w^4)(1+1) & = & 2.\\ \end{aligned}\]

Assim,

\[\begin{aligned} p_{2000}(w) & = & \\ \prod_{k=0}^{399} \prod_{j=1}^{5}(1+w^{5k+j}) &=& \\ \prod_{k=0}^{399} 2 & = & 2^{200}. \\ \end{aligned}\]

De modo análogo, podemos provar que \[p_{2000}(w^2)=p_{2000}(w^3) = p_{2000}(w^4) = 2^{400}.\]

Além disso, é fácil ver que $p_{2000}(1) = 2^{2000}$. Como $1^k+w^k+w^{2k}+w^{3k}+w^{4k}=0$, se $5 \nmid k$, e $5$ em caso contrário, se $l=\frac{2000\cdot 2001}{2}$ e

\[\displaystyle p_{2000}(x) = \sum_{i=0}^{l} a_ix^i,\]

segue que

\[\begin{aligned} \displaystyle \sum_{j=0}^{4} p_{2000}(w^j) & = & \\ \sum_{i=0}^{l} a_i (1+w^i+w^{2i}+w^{3i}+w^{4i}) & = & \\ \sum_{i \equiv 0 \pmod 5} 5a_i. && \end{aligned}\]

Finalmente, o número que procuramos é dado por

\[\begin{aligned} \displaystyle \sum_{i \equiv 0 \pmod 5} a_i & = & \dfrac{1}{5} \sum_{j=0}^{4}p_{2000}(w^j)\\ & = & \dfrac{2^{2000}+4 \cdot 2^{400}}{5}. \end{aligned}\]

A solução do problema original

Para resolver o problema original, novamente vamos considerar uma numeração para as linhas e colunas do tabuleiro como em uma matriz $8 \times 8$, mas dessa vez vamos associar a cada quadradinho $(ij)$ o monômio $x^iy^j$. A soma de todos os monômios escritos nas casas do tabuleiro gera o polinômio

\[\begin{aligned} p(x,y) & = & (x+x^2+\ldots +x^8)(y+y^2+\ldots +y^8) \\ & = & xy \cdot \dfrac{x^8-1}{x-1} \cdot \dfrac{y^8-1}{y-1}. \end{aligned}\]

Considere agora uma cobertura qualquer do tabuleiro e suponha que o monominó ocupa a casa $(ab)$. Se um triminó na posição horizontal tem como casa do canto esquerdo a posição $(ij)$, a soma dos seus monômios associados é \[x^{i}y^{j}+x^{i+1}y^{j}+x^{i+2}y^{j} = x^{i}y^{j}(1+x+x^2).\] Portanto, a soma de todos os monômios em peças na horizontal corresponde a um polinômio múltiplo de $(1+x+x^2)$, digamos o $(1+x+x^2)q_1(x,y)$. De modo análogo, a soma de todos os monômios escritos nas peças na vertical é um polinômio múltiplo de $1+y+y^2$, que denotaremos por $(1+y+y^2)q_2(x,y)$. Assim,

\[p(x,y) = (1+x+x^2)q_1(x,y) + (1+y+y^2)q_2(x,y) + x^ay^b.\]

Seja $w = \,\mbox{$\rm{cis}\,$}\frac{2\pi}{3}$. Como $1+w+w^2=0$, podemos concluir que

\[\begin{aligned} w^aw^b & = & p(w,w) \\ & = & w^2 \dfrac{w^8-1}{w-1} \cdot \dfrac{w^8-1}{w-1} \\ & = & w^2 \dfrac{w^2-1}{w-1} \cdot \dfrac{w^2-1}{w-1} \\ & = & w^2 (w+1)^2 \\ & = & 1 \end{aligned}\] e \[\begin{aligned} w^aw^{2b} & = & p(w,w^2) \\ & = & w^3 \dfrac{w^8-1}{w-1} \cdot \dfrac{w^{16}-1}{w^2-1} \\ & = & \dfrac{w^2-1}{w-1} \cdot \dfrac{w-1}{w^2-1} \\ & = & 1. \end{aligned}\]

Como $w^k=1$ apenas quando $k$ é um múltipo de $3$, podemos concluir que $a+b$ e $a+2b$ são multiplos de $3$ e, consequentemente, $a$ e $b$ são múltiplos de $3$. Isso nos diz que as únicas posições que podem receber o monominó em uma cobertura são as que estão pintadas de laranja na próxima figura e representam as posições $(3,3)$, $(3,6)$, $(6,3)$ e $(6,6)$.

Para verificar que todas elas são possíveis, perceba que a primeira cobertura apresentada no enunciado nos garante que uma delas é admissível. Agora perceba que basta rodar o tabuleiro três vezes por $90^{\circ}$ no sentido horário para obter coberturas para as outras três posições. Isso conclui a solução.

Exercícios e sugestões de leituras

Exercício 5. (IME) Mostre que \[\displaystyle \sum_{k \equiv 0 \pmod 3} {n \choose k} = \dfrac{1}{3} \left [ 2^n + 2\cos (n\pi/3) \right ].\]

Dica: Seja $q(x)=(1+x)^n$ e $w = \,\mbox{$\rm{cis}\,$}\frac{2\pi}{3}$. Quanto vale $q(1)+q(w)+q(w^2)$?

Exercício 6. (IMO 1974) Prove que o número \[\sum_{k=0}^n {2n+1 \choose 2k+1}2^{3k}\] não é divisível por $5$ para qualquer inteiro $n \geq 0$.
Dica: Perceba que $2^3 \equiv -2 \pmod 5$ e que a soma dada tem o mesmo resto que $\sum_{k=0}^n {2n+1 \choose 2k+1}(-2)^{k}$ na divisão por $5$. Em seguida, faça a expansão binomial do número $(1+i\sqrt{2})^{2n+1}$.

Exercício 7. (Olimpíada de São Petesburgo) A sequência finita $a_1,a_2, \ldots, a_n$ é chamada $p$-balanceada se qualquer soma da forma $a_k+a_{k+p}+a_{k+2p}+ \ldots$ é a mesma para qualquer $k=1,2, \ldots, p$. Prove que se a sequência com 50 membros é $p$-balanceada para $p=3,5,7,11,13,17$ então todos estes números são iguais a zero.

Exercício 8. (Fórmula da Multisecção) Se $f(x)=\sum_k a_kx^k$, mostre que \[\displaystyle \sum_{k \equiv r \pmod m} a_kx^k = \dfrac{1}{m} \sum_{s=0}^{m-1}w^{-rs}f(w^sx),\] em que $w=e^{2\pi i/m}$.

Uma pergunta interessante que poderia ser feita na linha da discussão do problema original é determinar de quantos modos podemos cobrir o tabuleiro $8\times 8$ com $21$ triminós e $1$ monominó?

Para um tabuleiro $8 \times 8$ sendo coberto apenas com dominós, que são peças $2 \times 1$, existem $12988816$ coberturas dele com $32$ dominós. A figura anterior ilustra uma delas. Na referência o leitor poderá encontrar a seguinte (surpreendente) fórmula para o número de coberturas de um tabuleiro $m \times n$ com dominós: \[\left [ \prod_{k=1}^{m} \prod_{l=1}^{n} \left ( 2 \cos \frac{\pi k}{m+1} + 2i \cos \frac{\pi l}{n+1}\right ) \right ]^{1/2}.\] O problema original é da referência . Para aplicações de raízes da unidade, como no Teorema de Klarner, recomendamos o capítulo $13$ do excelente .

Bibliografia

A. C. Muniz Neto, An Excursion Through Elementary Mathematics, Volume III: Discrete Mathematics and Polynomial Algebra, 1st ed. Springer, 2018.

R. Honsberger, In Polya’s Footsteps: Miscellaneous Problems and Essays, Mathematical Association of America, 1997.

E. Lozansky and C. Rousseau, Winning Solutions, 1st ed. Springer, 1996.

T. Andreescu, Z. Feng, and G. Yu, Mathematical Olympiads 2000-2001: Problems and Solutions from Around the World, 1st ed. Mathematical Association of America, 2003.

J. Matousek and J. Nesetril, Thirty-three Miniatures: Mathematical and Algorithmic Applications of Linear Algebra, American Mathematical Society, 2010.

Samuel Feitosa é professor na Universidade Federal da Bahia desde 2012. Foi medalhista de Bronze na Olimpíada Internacional de Matemática em 2003 e é membro da Comissão Nacional de Olimpíadas de Matemática da Sociedade Brasileira de Matemática (SBM). Contribui ativamente na organização de olimpíadas e treinamentos de alunos para diversas competições matemáticas nacionais e internacionais.

\(\times\)	\(w^0\)	\(w^1\)	\(w^2\)
\(w^0\)	\(w^0\)	\(w^1\)	\(w^2\)
\(w^1\)	\(w^1\)	\(w^2\)	\(w^0\)
\(w^2\)	\(w^2\)	\(w^0\)	\(w^1\)