Problema
Contando Paralelogramos e Outros Problemas
Ao contrário de outras áreas da atividade humana, um Problema em Matemática pode ser uma fonte de diversão. Nesta seção, convidamos os leitores a pensarem em algums problemas, de variados níveis de dificuldade, e a enviarem suas soluções para serem publicadas nas próximas edições.
Problemas Universitários
Problema 1. Uma malha triangular é formada pela decomposição de um triângulo equilátero de lado \(5\) em \(5^2\) triângulos equiláteros de lado \(1\), como indicado na figura. Determine o número de paralelogramos que podem ser desenhados por segmentos que formam a malha.
Problema 2. Determine a quantidade de números reais \(x\) que satisfazem a equação: \[2^{x^2+x} + \log_2 x = 2^{x+1}.\]
Problema 3. Seja \(a\) um inteiro positivo tal que
\[1+\dfrac{1}{2}+\dfrac{1}{3}+\ldots +\dfrac{1}{25} = \dfrac{a}{25!}.\]
Encontre o resto de \(a\) na divisão por \(13\).
Problema 4. Um hexágono regular de lado \(1\) está inscrito na interseção de duas parábolas idênticas, mas que estão orientadas em direções opostas, i.e., uma é simétrica a outra em relação à reta que passa pelos seus pontos de interseção. Encontre a área da região sombreada, ou seja, a área que está entre as parábolas, mas que é externa ao hexágono.

Problema 5. Calcule o valor da soma \[\displaystyle S = \sum_{k=1}^{2022} (-1)^k \cdot \dfrac{(k^2+k+1)}{k!}.\]
Problema 6. Sejam \(a\) e \(b\) números reais com \(a<b\) e sejam \(f,g:\left[a,b\right] \rightarrow \left(0, +\infty\right)\) funções contínuas tais que \(\int_{a}^{b} f(x)dx = \int_{a}^{b}g(x)dx\), mas \(f\neq g\). Defina \[I_{n} = \int_{a}^{b}\frac{\left(f(x)\right)^{n+1}}{\left(g(x)\right)^{n}}dx \text{, } \forall n\in \mathbb{N}.\] Mostre que a sequência \(\left(I_{n}\right)_{n\in \mathbb{N}}\) é crescente e que \(\lim_{n\rightarrow +\infty} I_{n} = +\infty\).
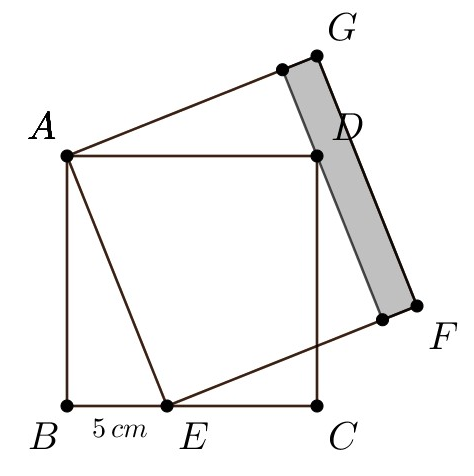
Problema 7. Na figura a seguir, \(ABCD\) e \(AEFG\) são quadrados. O segmento \(BE\) mede \(5\,cm\). Encontre a área do retângulo sombreado.
Problema 8. Na figura a seguir, cada quadradinho representa uma cadeira. Note que as quantidades de cadeiras consecutivas de uma mesma cor correspondem apenas aos números \(1\) e \(3\), que são ímpares.

De quantas maneiras podemos colocar \(12\) cadeiras em fila, cada uma sendo da cor branca ou cinza, de tal modo que as quantidades de cadeiras consecutivas pintadas de uma mesma cor sejam sempre números ímpares?
Problema 9. Na figura a seguir, \(X\) é um ponto no interior do triângulo equilátero \(ABC\) e \(Y\), \(W\) e \(Z\) são os pés das perpendiculares de \(X\) aos lados \(AC\), \(BC\) e \(AB\), respectivamente.
Se \(XY=k\), \(XZ=2k\), \(XW = 4k\) e a área do quadrilátero \(AYXZ\) é \(13\,cm^2\), encontre a área do triângulo \(ABC\).
Se \(XY=ak\), \(XZ=bk\) e \(XW = ck\), encontre a razão entre as áreas do triângulo \(ABC\) e do quadrilátero \(AYXZ\).

Caso queira compartilhar sua solução de alguns dos problemas acima
com nossos leitores, envie uma mensagem com o seu texto e nome completo
para hipatia@ufba.br.
